【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
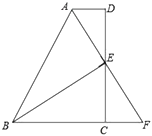
(1)求证:△ADE≌△FCE.
(2)若![]() ,求证:
,求证:![]() .
.
(3)在(2)的条件下,若![]() ,
,![]() ,
,![]() ,
,![]() ,则点
,则点![]() 到
到![]() 的距离是______.(直接写出结果即可,不用写出过程)
的距离是______.(直接写出结果即可,不用写出过程)
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据皮皮虾的性质可得![]() ,由E是CD中点可得DE=EC,利用ASA即可证明△ADE≌△FCE;(2)根据全等三角形的性质可得
,由E是CD中点可得DE=EC,利用ASA即可证明△ADE≌△FCE;(2)根据全等三角形的性质可得![]() ,
,![]() ,由AB=BC+AD可得AB=BF,利用SSS可证明△ABE≌△FBE,即可得出∠AEB=∠FEB=90°,可得结论;(3)作EH⊥AB,可得EH的长为点E到AB的距离,根据全等三角形的性质可得AE=EF,AB=BF,利用面积法求EH的长即可得答案.
,由AB=BC+AD可得AB=BF,利用SSS可证明△ABE≌△FBE,即可得出∠AEB=∠FEB=90°,可得结论;(3)作EH⊥AB,可得EH的长为点E到AB的距离,根据全等三角形的性质可得AE=EF,AB=BF,利用面积法求EH的长即可得答案.
(1)∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵在![]() 与
与![]() 中,
中,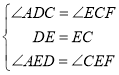 ,
,
∴△ADE≌△FCE(ASA).
(2)由(1)知△ADE≌△FCE,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 与
与![]() 中,
中,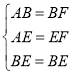 ,
,
∴△ABE≌△FBE(SSS),
∴![]() ,
,
∴![]() .
.
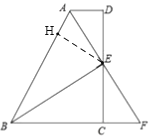
(3)如图,作EH⊥AB,
∴点E到AB的距离为EH的长,
∵在(2)的条件下有△ABE≌△FBE,![]() ,
,![]() ,
,
∴AE=EF=5,AB=BF=13,
∵由(2)得BE⊥AF,
∴S△ABE=![]() AB·EH=
AB·EH=![]() AE·BE,
AE·BE,
∵BE=12,
∴![]() ,
,
∴![]() ,
,
∴点![]() 到
到![]() 的距离为
的距离为![]() .
.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
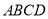 中,
中,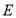 为
为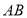 的中点,
的中点,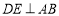 于点
于点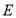 ,
,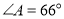 ,
,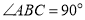 ,
,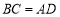 ,则
,则 的大小为______.(提示:一个三角形中有两条边相等,那么这两条边所对的角也相等)
的大小为______.(提示:一个三角形中有两条边相等,那么这两条边所对的角也相等)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在梯形
 中,
中, ,
, ,
, 的平分线
的平分线 交
交 于点
于点 ,连接
,连接 .
.
 求证:四边形
求证:四边形 是菱形;
是菱形; 若
若 ,
, ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
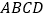 为矩形,四边形
为矩形,四边形 为菱形.
为菱形.
 求证:
求证: ;
; 试探究:当矩形
试探究:当矩形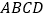 边长满足什么关系时,菱形
边长满足什么关系时,菱形 为正方形?请说明理由.
为正方形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
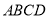 ,
,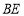 、
、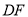 分别平分四边形的外角
分别平分四边形的外角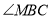 和
和 ,设
,设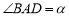 ,
, .
.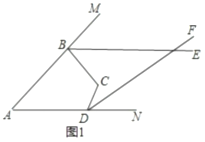
(1)如图1,若
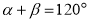 ,求
,求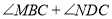 的度数;
的度数;(2)如图1,若
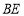 与
与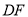 相交于点
相交于点 ,
,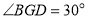 ,请写出
,请写出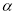 、
、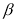 所满足的等量关系式;
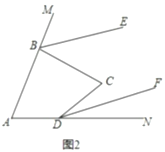
所满足的等量关系式;(3)如图2,若
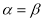 ,判断
,判断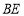 、
、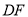 的位置关系,并说明理由.
的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平 路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明 上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是( )分钟
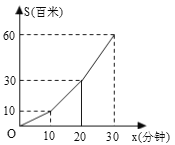
A.30 分钟B.38
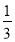 分钟C.41
分钟C.41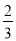 分钟D.43
分钟D.43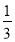 分钟
分钟 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
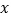 的一元二次方程
的一元二次方程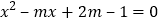 的两个实数根的平方和为
的两个实数根的平方和为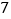 ,那么
,那么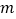 的值是( )
的值是( )A. 5 B. -1 C. 5或-1 D. -5或1
相关试题

