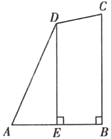
【题目】如图,在四边形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的大小为______.(提示:一个三角形中有两条边相等,那么这两条边所对的角也相等)
的大小为______.(提示:一个三角形中有两条边相等,那么这两条边所对的角也相等)
参考答案:
【答案】![]()
【解析】
由E是AB中点可得AE=BE,由DE⊥AB可得∠AED=∠BED=90°,理由SAS可证明△AED≌△BED,可得BD=AD,∠EBD=∠A,可求出∠DBC的度数,根据AD=BC可得BC=BD,即可得出∠C=∠BDC,根据三角形内角和定理求出∠C的度数即可.
∵E是AB中点,
∴AE=BE,
∵DE⊥AB,
∴∠AED=∠BED=90°,
在△AED和△BED中,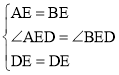 ,
,
∴△AED≌△BED,
∴BD=AD,∠EBD=∠A=66°,
∵∠ABC=90°,
∴∠DBC=90°-66°=24°,
∵AD=BC,
∴BD=BC,
∴∠C=∠BDC=![]() (180°-∠DBC)=78°.
(180°-∠DBC)=78°.
故答案为:78°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, ,
, ,点
,点 为
为 的中点.如果点
的中点.如果点 在线段
在线段 上以
上以 的速度由点
的速度由点 向
向 点运动,同时,点
点运动,同时,点 在线段
在线段 上由点
上由点 向
向 点运动.
点运动.
(1)若点
 的运动速度与点
的运动速度与点 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后, 与
与 是否全等,请说明理由.
是否全等,请说明理由.(2)若点
 的运动速度与点
的运动速度与点 的运动速度不相等,当点
的运动速度不相等,当点 的运动速度为多少时,能够使
的运动速度为多少时,能够使 与
与 全等?
全等? -
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有
 个相同小球,分别标有不等的自然数
个相同小球,分别标有不等的自然数 、
、 、
、 、
、 ,小丽每次从袋中同时摸出
,小丽每次从袋中同时摸出 个小球,并计算摸出的这
个小球,并计算摸出的这 个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:
个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:摸球总次数









“和为
 ”出现的频数
”出现的频数




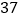

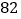


“和为
 ”出现的频率
”出现的频率









 如果实验继续进行下去,出现“和为
如果实验继续进行下去,出现“和为 ”的频率将稳定在它的概率附近.试估计出现“和为
”的频率将稳定在它的概率附近.试估计出现“和为 ”的概率;
”的概率; 根据
根据 中结论,求出自然数
中结论,求出自然数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】画
 ,使
,使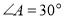 ,
,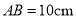 ,
, 的对边只能在长度分别为
的对边只能在长度分别为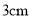 、
、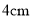 、
、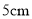 、
、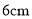 的四条线段中任选,可画出不同形状的三角形的个数是( )(提示:在直角三角形中,如果一个锐角等于
的四条线段中任选,可画出不同形状的三角形的个数是( )(提示:在直角三角形中,如果一个锐角等于 ,那么它所对的直角边是斜边的一半)
,那么它所对的直角边是斜边的一半)A.2个B.3个C.4个D.6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在梯形
 中,
中,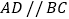 ,
, ,
, 的平分线
的平分线 交
交 于点
于点 ,连接
,连接 .
.
 求证:四边形
求证:四边形 是菱形;
是菱形; 若
若 ,
, ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
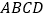 为矩形,四边形
为矩形,四边形 为菱形.
为菱形.
 求证:
求证: ;
; 试探究:当矩形
试探究:当矩形 边长满足什么关系时,菱形
边长满足什么关系时,菱形 为正方形?请说明理由.
为正方形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
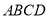 中,
中,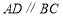 ,
, 为
为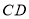 的中点,连接
的中点,连接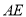 、
、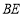 ,延长
,延长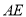 交
交 的延长线于点
的延长线于点 .
.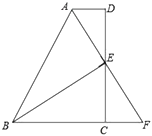
(1)求证:△ADE≌△FCE.
(2)若
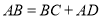 ,求证:
,求证: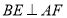 .
.(3)在(2)的条件下,若
 ,
, ,
,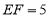 ,
,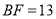 ,则点
,则点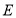 到
到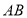 的距离是______.(直接写出结果即可,不用写出过程)
的距离是______.(直接写出结果即可,不用写出过程)
相关试题

