【题目】完成下面推理过程: 如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE=()
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ![]() ()
()
∠ABE= ![]() ()
()
∴∠ADF=∠ABE
∴∥()
∴∠FDE=∠DEB.()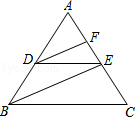
参考答案:
【答案】∠ABC;两直线平行,同位角相等;∠ADE;角平分线定义;∠ABC;角平分线定义;DF;BE;同位角相等,两直线平行;两直线平行,内错角相等
【解析】解:理由是:∵DE∥BC(已知), ∴∠ADE=∠ABC(两直线平行,同位角相等),
∵DF、BE分别平分ADE、∠ABC,
∴∠ADF= ![]() ∠ADE(角平分线定义),
∠ADE(角平分线定义),
∠ABE= ![]() ∠ABC(角平分线定义),
∠ABC(角平分线定义),
∴∠ADF=∠ABE,
∴DF∥BE(同位角相等,两直线平行),
∴∠FDE=∠DEB(两直线平行,内错角相等),
所以答案是:∠ABC,两直线平行,同位角相等;∠ADE,角平分线定义;∠ABC,角平分线定义;DF,BE,同位角相等,两直线平行;两直线平行,内错角相等.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果a为最大的负整数,b为绝对值最小的数,c为最小的正整数,则a﹣b+c的值是( )
A. ﹣1 B. 0 C. 1 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
 .
.(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春天来了,小颖要用总长为12米的篱笆围一个长方形花圃,其一边靠墙(墙长9米),另外三边是篱笆,其中BC不超过9米.设垂直于墙的两边AB,CD的长均为x米,长方形花圃的面积为y米2 .

(1)用x表示花圃的一边BC的长,判断x=1是否符合题意,并说明理由;
(2)求y与x之间的关系式;
根据关系式补充表格:x(米)
…
1.5
2
2.5
3
3.5
4
4.5
…
y(米2)
…
13.5
16
17.5
17.5
13.5
…
观察表中数据,写出y随x变化的一个特征: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内一点P(2,-3)关于原点对称点的坐标是( )
A.(3,-2) B.(2,3) C.(-2,3) D.(2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(1,m)在第四象限,则点Q(-1,m)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是边长为4的正方形,点P从点O沿边OA向点A运动,每秒运动1个单位.连结CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点E作EF∥OA,交OB于点F,连结FD、BE,设点P运动的时间为
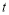
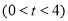 .
.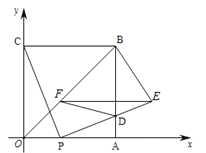
(1)点E的坐标为 (用含
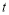 的代数式表示);
的代数式表示);(2)试判断线段EF的长度是否随点P的运动变化而改变?并说明理由;
(3)当
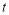 为何值时,四边形BEDF的面积为
为何值时,四边形BEDF的面积为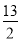 .
.
相关试题

