【题目】如图,四边形OABC是边长为4的正方形,点P从点O沿边OA向点A运动,每秒运动1个单位.连结CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点E作EF∥OA,交OB于点F,连结FD、BE,设点P运动的时间为![]()
![]() .
.
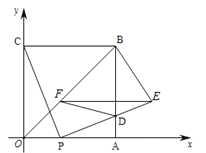
(1)点E的坐标为 (用含![]() 的代数式表示);
的代数式表示);
(2)试判断线段EF的长度是否随点P的运动变化而改变?并说明理由;
(3)当![]() 为何值时,四边形BEDF的面积为
为何值时,四边形BEDF的面积为![]() .
.
参考答案:
【答案】(1)、(4+t,t);(2)、不变,理由见解析;(3)、t=1或3.
【解析】
试题分析:(1)、过点E作EH⊥OA,垂足为H,从而得出点E的坐标;(2)、根据题意得出OA=OB=4,然后得出点F的坐标,根据点的坐标得出EF的长度;(3)、根据△DAP∽△POC得出BD的长度,然后根据四边形的面积列出方程得出答案.
试题解析:(1)、过点E作EH⊥OA,垂足为H. 点E的坐标为(4+![]() ,
,![]() ).
).
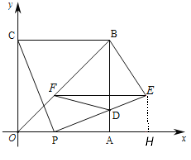
(2)、线段EF的长度不变.理由如下:
由题意知:OA=OB=4,∴点B坐标为(4,4),∠BOA=45°
∵EF∥OA,点E为(4+![]() ,
,![]() ),点F的坐标为(
),点F的坐标为(![]() ,
,![]() ) ∴EF=
) ∴EF=![]() =4,即线段EF的长度不变.
=4,即线段EF的长度不变.
(3)、由(1)知:∠DPA=∠PCO,又∠DAP=∠POC=90°
∴△DAP∽△POC,∴![]() ,∵OP=
,∵OP=![]() ,OC=4,∴AP=4-
,OC=4,∴AP=4-![]()
∴![]() ,∴AD=
,∴AD=![]() ,∴BD=
,∴BD=![]() =
=![]() ∵EF∥OA,AB⊥OA;∴EF⊥BD
∵EF∥OA,AB⊥OA;∴EF⊥BD
∵S四边形BEDF=![]() =
=![]() =
=![]()
解得t=1或t=3.所以,当![]() 为1、3时,四边形BEDF的面积为
为1、3时,四边形BEDF的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程: 如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE=()
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ()
()
∠ABE= ()
()
∴∠ADF=∠ABE
∴∥()
∴∠FDE=∠DEB.()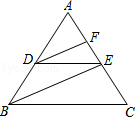
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内一点P(2,-3)关于原点对称点的坐标是( )
A.(3,-2) B.(2,3) C.(-2,3) D.(2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(1,m)在第四象限,则点Q(-1,m)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】江苏是全国首个自然村“村村通宽带”省份.我市某村为了将当地农产品外销,建立了淘宝网店.该网店于今年7月底以每袋25元的成本价收购一批农产品.当商品售价为每袋40元时,8月份销售256袋.9、10月该商品十分畅销.销售量持续走高.在售价不变的基础上,10月份的销售量达到400袋.设9、10这两个月月平均增长率不变.
(1)求9、10这两个月的月平均增长率;
(2)为迎接双“十一”,11月份起,该网店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/每袋,销售量就增加5袋,当农产品每袋降价多少元时,该淘宝网店11月份获利4250元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为
 米.
米.(1)如果通道所占面积是整个长方形空地面积的
 ,求出此时通道的宽;
,求出此时通道的宽;(2)能否设计出符合题目要求,且长方形花圃的形状与原长方形空地的形状相似的花圃?若能,求出此时通道的宽;若不能,则说明理由.

相关试题

