【题目】如图,一圆弧形桥拱的圆心为![]() ,拱桥的水面跨度
,拱桥的水面跨度![]() 米,桥拱到水面的最大高度
米,桥拱到水面的最大高度![]() 为
为![]() 米.求:
米.求:

![]() 桥拱的半径;
桥拱的半径;
![]() 现水面上涨后水面跨度为
现水面上涨后水面跨度为![]() 米,求水面上涨的高度为________米.
米,求水面上涨的高度为________米.
参考答案:
【答案】(1)50;(2)10.
【解析】
(1)根据垂径定理和勾股定理求解;
(2)由垂径定理求出MH,由勾股定理求出EH,得出HF即可.
(1)如图,
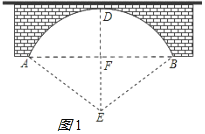
设点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
则由垂径定理知,点F是AB的中点,AF=FB=![]() AB=40,EF=ED-FD=AE-DF,
AB=40,EF=ED-FD=AE-DF,
由勾股定理知,AE2=AF2+EF2=AF2+(AE-DF)2,
设圆的半径是r,
则:r2=402+(r-20)2,
解得:r=50;
即桥拱的半径为50米;
(2)设水面上涨后水面跨度MN为60米,MN交ED于H,连接EM,如图2所示
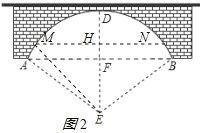
则MH=NH=![]() MN=30,
MN=30,
∴EH=![]() =40(米),
=40(米),
∵EF=50-20=30(米),
∴HF=EH-EF=10(米);
故答案为:10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若六边形
 是
是 的内接正六边形,则
的内接正六边形,则 ________,
________, ________,
________, ________,
________, ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确( )?

A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两个螺丝间的距离的最大值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MAN是一个钢架结构,在角内部最多只能构造五根等长钢条,则∠ABC的度数最大为_______度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 的直径,
的直径, 于点
于点 ,
, 是弧AC上的动点,连接
是弧AC上的动点,连接 分别交
分别交 ,
, 于点
于点 ,
, .
.
 当
当 时,
时, 与
与 相等吗?为什么?
相等吗?为什么? 当点
当点 在什么位置时,
在什么位置时, ?证明你的结论.
?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
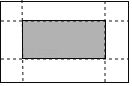
A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
相关试题

