【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点![]() ,
,![]() 是弧AC上的动点,连接
是弧AC上的动点,连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

![]() 当
当![]() 时,
时,![]() 与
与![]() 相等吗?为什么?
相等吗?为什么?
![]() 当点
当点![]() 在什么位置时,
在什么位置时,![]() ?证明你的结论.
?证明你的结论.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)由圆周角定理知:AB⊥AC,在Rt△ABC中,AD⊥BC,易证得∠BAD=∠C,已知PA=AB,可得∠ABE=∠C,所以∠ABE=∠BAD,即AE=BE;
(2)当AF=EF时,∠FAE=∠FEA,易得∠FAE=∠ABD,∠FEA=∠DEB,因此∠BED=∠ABD,那么它们的余角也相等,即∠FBC=∠BAD,由(1)知∠BAD=∠C,即∠FBC=∠C,那么弧PC=弧AB,因此当弧PC=弧AB时,AF=EF.
![]() 证明:∵
证明:∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ;
;
![]() 当弧
当弧![]() 弧
弧![]() 时,
时,![]() ,
,
证明:∵弧![]() 弧
弧![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依次为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两个螺丝间的距离的最大值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一圆弧形桥拱的圆心为
 ,拱桥的水面跨度
,拱桥的水面跨度 米,桥拱到水面的最大高度
米,桥拱到水面的最大高度 为
为 米.求:
米.求:
 桥拱的半径;
桥拱的半径; 现水面上涨后水面跨度为
现水面上涨后水面跨度为 米,求水面上涨的高度为________米.
米,求水面上涨的高度为________米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MAN是一个钢架结构,在角内部最多只能构造五根等长钢条,则∠ABC的度数最大为_______度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
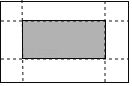
A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/kg.在乙批发店,一次购买数量不超过50kg时,价格均为7元/kg;一次性购买超过50kg时,其中有50kg的价格仍为7元/kg,超过50kg的部分价格为5元/kg.设小王在同一个批发店一次购买苹果的数量为
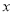 kg(
kg(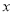 >0)
>0)(1)根据题意填表:a= b=
一次购买数量(kg)
30
50
150
…
甲批发店花费(元)
180
300
900
…
乙批发店花费(元)
a
350
b
…
(2)设在甲批发店花费
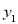 元,在乙批发店花费
元,在乙批发店花费 元,分别求
元,分别求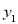 ,
, 关于
关于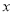 的函数解析式;
的函数解析式;(3)若小王在同一个批发店一次性购买苹果花费了360元,则他在甲、乙两个批发店中批发,哪个批发店购买数量多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形
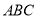 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: )
)例2 等腰三角形
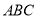 中,
中, ,求
,求 的度数.(答案:
的度数.(答案: 或
或 或
或 )
)张老师启发同学们进行变式,小敏编了如下两题:
变式1: 等腰三角形
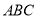 中,∠A=100°,求
中,∠A=100°,求 的度数.
的度数.变式2: 等腰三角形
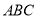 中,∠A= 45° ,求
中,∠A= 45° ,求 的度数.
的度数.(1)请你解答以上两道变式题.
(2)解(1)后,小敏发现,
 的度数不同,得到
的度数不同,得到 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形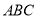 中,设
中,设 ,当
,当 只有一个度数时,请你探索
只有一个度数时,请你探索 的取值范围.
的取值范围.
相关试题

