【题目】如图,△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=α,AC、BD交于M
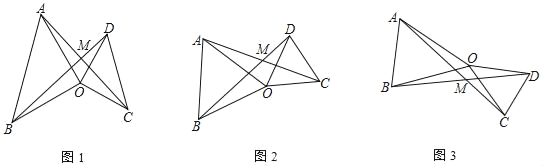
(1)如图1,当α=90°时,∠AMD的度数为 °
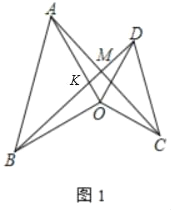
(2)如图2,当α=60°时,∠AMD的度数为 °
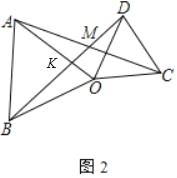
(3)如图3,当△OCD绕O点任意旋转时,∠AMD与α是否存在着确定的数量关系?如果存在,请你用表示∠AMD,并图3进行证明;若不确定,说明理由.
参考答案:
【答案】(1)90;(2)60;(3)∠AMD=180°﹣α,证明详见解析.
【解析】
(1)如图1中,设OA交BD于K.只要证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,可得∠AMK=∠BOK=90°;
(2)如图2中,设OA交BD于K.只要证明△BOD≌△AOC,推出∠OBD=∠OAC,由∠AKM=∠BKO,推出∠AMK=∠BOK=60°;
(3)如图3中,设OA交BD于K.只要证明△BOD≌△AOC,可得∠OBD=∠OAC,由∠AKO=∠BKM,推出∠AOK=∠BMK=α.可得∠AMD=180°-α.
(1)如图1中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=90°.
故答案为90.
(2)如图2中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKM=∠BKO,
∴∠AMK=∠BOK=60°.
故答案为60.
(3)如图3中,设OA交BD于K.
∵OA=OB,OC=OD,∠AOB=∠COD=α,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴∠OBD=∠OAC,
∵∠AKO=∠BKM,
∴∠AOK=∠BMK=α.
∴∠AMD=180°﹣α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上A,B两点对应的有理数分别为xA=﹣5和xB=6,动点P从点A出发,以每秒1个单位的速度沿数轴在A,B之间往返运动,同时动点Q从点B出发,以每秒2个单位的速度沿数轴在B,A之间往返运动.设运动时间为t秒.
(1)当t=2时,点P对应的有理数xP=______,PQ=______;
(2)当0<t≤11时,若原点O恰好是线段PQ的中点,求t的值;
(3)我们把数轴上的整数对应的点称为“整点”,当P,Q两点第一次在整点处重合时,直接写出此整点对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 ﹣2sin60°+(
﹣2sin60°+( 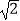 ﹣π)0﹣(
﹣π)0﹣(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
 中,
中, =4cm,
=4cm, =3cm,
=3cm, 为
为 的中点.动点
的中点.动点 从
从 点出发,以每秒1cm的速度沿
点出发,以每秒1cm的速度沿 运动,最终到达点
运动,最终到达点 .若点
.若点 运动的时间为
运动的时间为 秒,则当
秒,则当 =________ 时,
=________ 时, 的面积等于4.5.
的面积等于4.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=
 ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.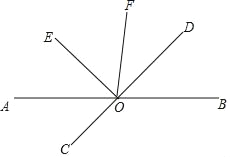
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=
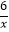 相交于点A(m,3),B(﹣6,n),与x轴交于点C.
相交于点A(m,3),B(﹣6,n),与x轴交于点C. 
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP= S△BOC , 求点P的坐标(直接写出结果).
S△BOC , 求点P的坐标(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题: 在某场CBA比赛中,某位运动员的技术统计如表所示:
技术
上场时间(分钟)
出手投篮(次)
投中
(次)罚球得分(分)
篮板
(个)助攻(次)
个人总得分(分)
数据
38
27
11
6
3
4
33
注:(i)表中出手投篮次数和投中次数均不包括罚球;
(ii)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.
相关试题

