搜索
【题目】列方程或方程组解应用题： 在某场CBA比赛中，某位运动员的技术统计如表所示：
技术 | 上场时间（分钟） | 出手投篮（次） | 投中 | 罚球得分（分） | 篮板 | 助攻（次） | 个人总得分（分） |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注：（i）表中出手投篮次数和投中次数均不包括罚球；
（ii）总得分=两分球得分+三分球得分+罚球得分．
根据以上信息，求本场比赛中该运动员投中两分球和三分球各几个．
参考答案：
【答案】解：设本场比赛中该运动员投中两分球x个，三分球y个， 根据题意得： 
，
解得： 
．
答：设本场比赛中该运动员投中两分球6个，三分球5个
【解析】设本场比赛中该运动员投中两分球x个，三分球y个，根据投中次数结合总分，即可得出关于x、y的二元一次方程组，解之即可得出结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M
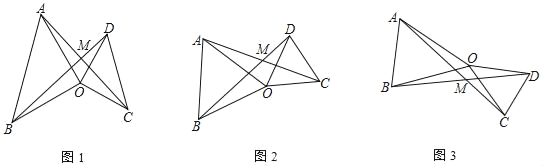
（1）如图1，当α＝90°时，∠AMD的度数为 °
（2）如图2，当α＝60°时，∠AMD的度数为 °
（3）如图3，当△OCD绕O点任意旋转时，∠AMD与α是否存在着确定的数量关系？如果存在，请你用表示∠AMD，并图3进行证明；若不确定，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB、CD相交于点O，OE⊥OD，OE平分∠AOF．
（1）∠BOD与∠DOF相等吗？请说明理由．
（2）若∠DOF=
∠BOE，求∠AOD的度数．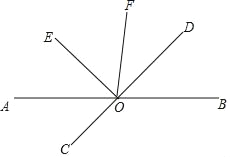
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y=kx+b（k≠0）与双曲线y=
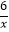相交于点A（m，3），B（﹣6，n），与x轴交于点C． 
（1）求直线y=kx+b（k≠0）的解析式；
（2）若点P在x轴上，且S△ACP=
S△BOC ， 求点P的坐标（直接写出结果）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，A（﹣2，0），B（0，4），以B点为直角顶点在第二象限作等腰直角△ABC．
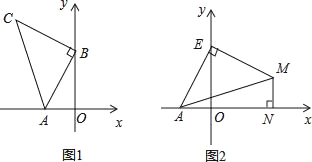
（1）求C点的坐标；
（2）在坐标平面内是否存在一点P，使△PAB与△ABC全等？若存在，求出P点坐标，若不存在，请说明理由；
（3）如图2，点E为y轴正半轴上一动点，以E为直角顶点作等腰直角△AEM，过M作MN⊥x轴于N，求OE﹣MN的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD为平行四边形，∠BAD的角平分线AF交CD于点E，交BC的延长线于点F．
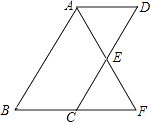
（1）求证：BF=CD；
（2）连接BE，若BE⊥AF，∠BFA=60°，BE=2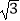
，求平行四边形ABCD的周长． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠ABC=120°，BD平分∠ABC，∠DAC=60°，若AB=2，BC=3，则BD的长是（ ）
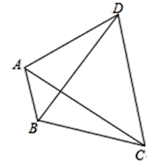
A. 5 B. 7 C. 8 D. 9
相关试题
