【题目】如图所示,一个工人师傅要将一个正方形ABCD的余料,修剪成四边形ABEF的零件,其中CE=![]() BC,F是CD的中点.
BC,F是CD的中点.
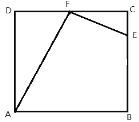
(1)若正方形的边长为a,试用含a的代数式表示AF2+EF2的值;
(2)连结AE,△AEF是直角三角形吗?为什么?(正方形的四条边都相等,四个角都是直角)
参考答案:
【答案】(1)见解析;(2)△AEF是直角三角形,理由见解析;
【解析】
(1)先连接AE,证明△ADF∽△FCE,得到∠AFE=90°,所以AF2+EF2=AE2=![]() a2.
a2.
(2)由(1)的结论利用勾股定理逆定理,即可解答.
(1)连接AE,
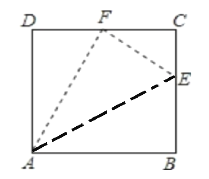
则AB=a,BE=![]() a,
a,
∵∠B=90°,
∴AE2=![]() a2;
a2;
∵CE:CF=DF:AD=1:2,
∠C=∠D=90°;
∴△ADF∽△FCE,
∴∠CFE+∠AFD=90°
∴∠AFE=90°
∴AF2+EF2=AE2=![]() a2;
a2;
(2) △AEF是直角三角形,理由如下:
由(1)中可知AF2+EF2=AE2,
∴△AEF是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=
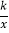 (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形中,点O为对角线BD的中点,DE、BF分别平分∠ADC和∠ABC.
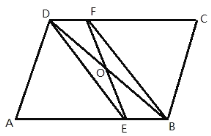
(1)求证:EF、BD互相平分;
(2)若∠A=60,AE=2EB,AD=4,求四边形DEBF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B,C三点共线,线段AB=20 cm,BC=8 cm,点E,F分别是线段AB,BC的中点,则线段EF的长为( )
A.28 cm或12 cmB.28 cmC.14 cmD.14cm或6 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在八年级上学期期中测试中各学科得分如下表,则下列判断正确的是( )
单元
语文
数学
英语
物理
历史
生物
地理
分数
85
80
92
80
85
95
85
A. 平均数是85B. 众数是85C. 中位数是80D. 方差是85
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,AB=AC=12cm,BC=9cm,若点Q在线段CA上以4cm/s的速度由点C向点A运动,点P在BC线段上以3cm/s的速度由B向C运动,求多长时间点Q与点P第一次在哪条边上相遇?( )
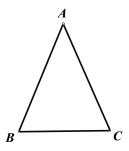
A.24s BC边B.12s BC边
C.24s AB边D.12s AC边
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论,其中,正确结论的个数是( )
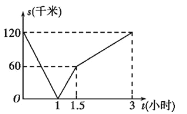
①出发1小时时,甲、乙在途中相遇;
②乙开车速度是80千米/小时;
③出发1.5小时时,乙比甲多行驶了60千米;
④出发3小时时,甲、乙同时到达终点;
A. 1B. 2C. 3D. 4
相关试题

