【题目】如图,圆锥的底面半径为10 cm,高为10![]() cm.
cm.
(1)求圆锥的全面积;
(2)若一只蚂蚁从底面上一点A出发绕圆锥侧面一周回到SA上的点M处,且SM=3AM,求它所走的最短距离.

参考答案:
【答案】(1)500π;(2)50 cm.
【解析】
解:(1)由题意,可得圆锥的母线SA=![]() =
=![]() =40(cm),
=40(cm),
∴S侧=π×10×40=400π(cm2),
S底=πAO2=100π(cm2),
∴S全=S侧+S底=(400+100)π=500π(cm2).
(2)沿母线SA将圆锥的侧面展开,如图,

则线段AM的长就是蚂蚁所走的最短距离.
由(1)知,SA=40 cm,![]() =20π cm.
=20π cm.
∵![]() =20π(cm),
=20π(cm),
∴n=![]() =90,
=90,
∴∠S=90°.
∵SA′=SA=40 cm,SM=3A′M,
∴SM=30 cm,
∴在Rt△ASM中,由勾股定理得AM=50 cm,
∴蚂蚁所走的最短距离是50 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB与直线CD相交于点O,OE平分
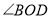 .
.
(1)如图①,若
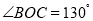 ,求
,求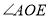 的度数;
的度数;(2)如图②,射线OF在
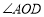 内部.
内部.①若
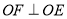 ,判断OF是否为
,判断OF是否为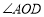 的平分线,并说明理由;
的平分线,并说明理由;②若OF平分
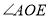 ,
,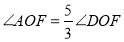 ,求
,求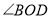 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义,如果一个四边形有一条对角线能将其分成一个等边三角形和一个直角三角形,那么这个四边形叫做等垂四边形,这条对角线叫做这个四边形的等垂对角线.
(1)已知
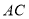 是四边形
是四边形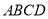 的等垂对角线,
的等垂对角线,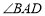 ,
,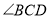 均为钝角,且
均为钝角,且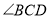 比
比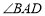 大
大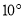 ,那么
,那么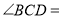 ________.
________.(2)如图,已知
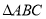 与
与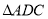 关于直线
关于直线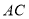 对称,
对称,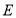 、
、 两点分别在
两点分别在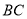 、
、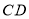 边上,
边上, ,
,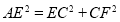 ,
,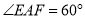 .求证:四边形
.求证:四边形 是等垂四边形。
是等垂四边形。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:

(1)a,b,c各表示几?
(2)这个几何体最少有几个小立方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体从左面看到的形状图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“四书五经”是中国的“圣经”,“四书五经”是《大学》、《中庸》、《论语》和《孟子》(四书)及《诗经》、《尚书》、《易经》、《礼记》、《春秋》(五经)的总称,这是一部被中国人读了几千年的教科书,包含了中国古代的政治理想和治国之道,是我们了解中国古代社会的一把钥匙,学校计划分阶段引导学生读这些书,计划先购买《论语》和《孟子》供学生使用,已知用500元购买《孟子》的数量和用800元购买《论语》的数量相同,《孟子》的单价比《论语》的单价少15元.
(1)求《论语》和《孟子》这两种书的单价各是多少?
(2)学校准备一次性购买这两种书
 本,但总费用不超过
本,但总费用不超过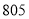 元,那么这所学校最多购买多少本《论语》?
元,那么这所学校最多购买多少本《论语》? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥底面圆的圆心,圆锥的高为2
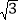 m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.(1)求∠ABC的度数;
(2)若∠ACP=2∠ABC,求光源A距水平面的高度.

相关试题

