【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,若AC=5,BC=12.求点D到AB的距离. 
参考答案:
【答案】解:如图,过点D作DE⊥AB于E,∵AC=5,BC=12,
∴AB= ![]() =13,
=13,
∵∠C=90°,AD是∠BAC的角平分线,
∴CD=DE,
在△ACD和△AED中,![]() ,
,
∴△ACD≌△AED(HL),
∴AE=AC=5,
BE=AB﹣AE=13﹣5=8,
设DE=x,
则BD=12﹣x,
在Rt△BDE中,DE2+BE2=BD2 ,
∴x2+82=(12﹣x)2 ,
解得x= ![]() .
.
答:点D到AB的距离是 ![]() .
.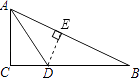
【解析】过点D作DE⊥AB于E,根据角平分线上的点到角的两边的距离相等可得CD=DE,然后利用“HL”证明△ACD和△AED全等,根据全等三角形对应边相等可得AE=AC,表示出BE,设DE=x,表示出BD,然后利用勾股定理列式计算即可得解.
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案,需要熟知定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为实现教育均衡发展,打造新优质学校,瑶海区计划对A、B两类薄弱学校全部进行改造,根据预算,共需资金1575万元.改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元,求改造一所A类学校和一所B类学校所需的资金分别是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商
﹣2÷2=﹣1
(2)请用你发现的规律求出图④中的数y和图⑤中的数x. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各多项式中,能用公式法分解因式的是( )
A. a2-b2+2ab B. a2+b2+ab C. 25n2+15n+9 D. 4a2+12a+9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km.

(1)牧童从A处将牛牵到河边P处饮水后再回到家C,试确定P在何处,所走路程最短?请在图中画出饮水的位置(保留作图痕迹),
不必说明理由.
(2)求出(1)中的最短路程. -
科目: 来源: 题型:
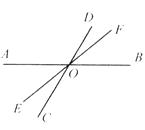
查看答案和解析>>【题目】如图所示,直线AB、CD、EF相交于点O,∠AOE=40°,∠BOC=2∠AOC,求∠DOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式3a2b﹣a3﹣1+ab2按a的升幂排列是 .
相关试题

