【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积(结果保留π和根号).
参考答案:
【答案】
(1)
解:∵∠B=60°,
∴△BOC是等边三角形,
∴∠1=∠2=60°,
∵OC平分∠AOB,
∴∠1=∠3,
∴∠2=∠3,
∴OA∥BD,
∴∠BDM=90°,∴∠OAM=90°,
∴AM是⊙O的切线
(2)
解:∵∠3=60°,OA=OC,
∴△AOC是等边三角形,
∴∠OAC=60°,
∵∠OAM=90°,
∴∠CAD=30°,
∵CD=2,
∴AC=2CD=4,
∴AD=2 ![]() ,
,
∴S阴影=S梯形OADC﹣S扇形OAC= ![]() (4+2)×2
(4+2)×2 ![]() ﹣
﹣ ![]() =6
=6 ![]() ﹣
﹣ ![]()
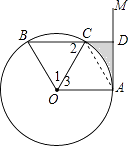
【解析】(1)由已知条件得到△BOC是等边三角形,根据等边三角形的性质得到∠1=∠2=60°,由角平分线的性质得到∠1=∠3,根据平行线的性质得到∠OAM=90°,于是得到结论;(2)根据等边三角形的性质得到∠OAC=60°,根据三角形的内角和得到∠CAD=30°,根据勾股定理得到AD=2 ![]() ,于是得到结论.
,于是得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣
 x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y= 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
(2)点P(2 ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,P点是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,设∠A、∠B、∠C的对边分别为a,b,c,过点A作AD⊥BC,垂足为D,会有sin∠C=
 ,则
,则
S△ABC= BC×AD=
BC×AD=  ×BC×ACsin∠C=
×BC×ACsin∠C=  absin∠C,
absin∠C,
即S△ABC= absin∠C
absin∠C
同理S△ABC= bcsin∠A
bcsin∠A
S△ABC= acsin∠B
acsin∠B
通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理:
如图2,在△ABC中,若∠A、∠B、∠C的对边分别为a,b,c,则
a2=b2+c2﹣2bccos∠A
b2=a2+c2﹣2accos∠B
c2=a2+b2﹣2abcos∠C
用上面的三角形面积公式和余弦定理解决问题:
(1)如图3,在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8.求S△DEF和DE2 .
解:S△DEF= EF×DFsin∠F=;
EF×DFsin∠F=;
DE2=EF2+DF2﹣2EF×DFcos∠F= .
(2)如图4,在△ABC中,已知AC>BC,∠C=60°,△ABC'、△BCA'、△ACB'分别是以AB、BC、AC为边长的等边三角形,设△ABC、△ABC'、△BCA'、△ACB'的面积分别为S1、S2、S3、S4 , 求证:S1+S2=S3+S4 .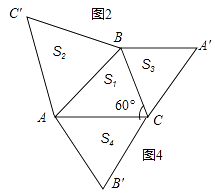
-
科目: 来源: 题型:
查看答案和解析>>【题目】△OPA和△OQB分别是以OP、OQ为直角边的等腰直角三角形,点C、D、E分别是OA、OB、AB的中点.

(1)当∠AOB=90°时如图1,连接PE、QE,直接写出EP与EQ的大小关系;
(2)将△OQB绕点O逆时针方向旋转,当∠AOB是锐角时如图2,(1)中的结论是否成立?若成立,请给出证明;若不成立,请加以说明.
(3)仍将△OQB绕点O旋转,当∠AOB为钝角时,延长PC、QD交于点G,使△ABG为等边三角形如图3,求∠AOB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点D,点B的坐标为(3,0),顶点C的坐标为(1,4).

(1)求二次函数的解析式和直线BD的解析式;
(2)点P是直线BD上的一个动点,过点P作x轴的垂线,交抛物线于点M,当点P在第一象限时,求线段PM长度的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为2 ?若存在求出点Q的坐标;若不存在请说明理由.
?若存在求出点Q的坐标;若不存在请说明理由.
相关试题

