【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( ) 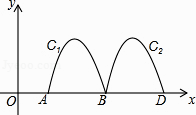
A.﹣2<m< ![]()
B.﹣3<m<﹣ ![]()
C.﹣3<m<﹣2
D.﹣3<m<﹣ ![]()
参考答案:
【答案】D
【解析】解:令y=﹣2x2+8x﹣6=0, 即x2﹣4x+3=0,
解得x=1或3,
则点A(1,0),B(3,0),
由于将C1向右平移2个长度单位得C2 ,
则C2解析式为y=﹣2(x﹣4)2+2(3≤x≤5),
当y=x+m1与C2相切时,
令y=x+m1=y=﹣2(x﹣4)2+2,
即2x2﹣15x+30+m1=0,
△=﹣8m1﹣15=0,
解得m1=﹣ ![]() ,
,
当y=x+m2过点B时,
即0=3+m2 ,
m2=﹣3,
当﹣3<m<﹣ ![]() 时直线y=x+m与C1、C2共有3个不同的交点,
时直线y=x+m与C1、C2共有3个不同的交点,
故选:D.
【考点精析】关于本题考查的二次函数图象的平移和抛物线与坐标轴的交点,需要了解平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE . 现给出下列命题:
(i)若 =
= 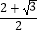 ,则tan∠EDF=
,则tan∠EDF= 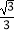
(ii)若DE2=BDEF,则DF=2AD
那么,下面判断正确的是( )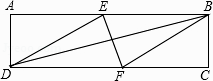
A.①正确,②正确
B.①正确,②错误
C.①错误,②正确
D.①错误,②错误 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数
 与方差s2如下表所示:
与方差s2如下表所示:甲
乙
丙
丁
平均数
 (cm)
(cm)561
560
561
560
方差s2
3.5
3.5
15.5
16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
-
科目: 来源: 题型:
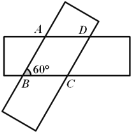
查看答案和解析>>【题目】如图,将两条宽度为3的直尺重叠在一起,使∠ABC=60°,则四边形ABCD的面积是_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形ABC中,AB=AC,∠B=30°,BC=
 cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.
cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.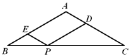
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 ﹣(﹣1)2015×(﹣
﹣(﹣1)2015×(﹣  )﹣2﹣|1﹣
)﹣2﹣|1﹣ 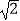 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个(分别标有1号、2号),黄球1个,从中任意摸出1球是绿球的概率是
 .
.
(1)试求口袋中绿球的个数;
(2)小明和小刚玩摸球游戏:第一次从口袋中任意摸出1球(不放回),第二次再摸出1球.两人约定游戏胜负规则如下:摸出“一绿一黄”,则小明赢;摸出“一红一黄”,则小刚赢.你认为这种游戏胜负规则公平吗?请用列表或画树状图的方法说明理由;若你认为不公平,请修改游戏胜负规则,使游戏变得公平.
相关试题

