【题目】一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个(分别标有1号、2号),黄球1个,从中任意摸出1球是绿球的概率是 ![]() .
.
(1)试求口袋中绿球的个数;
(2)小明和小刚玩摸球游戏:第一次从口袋中任意摸出1球(不放回),第二次再摸出1球.两人约定游戏胜负规则如下:摸出“一绿一黄”,则小明赢;摸出“一红一黄”,则小刚赢.你认为这种游戏胜负规则公平吗?请用列表或画树状图的方法说明理由;若你认为不公平,请修改游戏胜负规则,使游戏变得公平.
参考答案:
【答案】
(1)解:设绿球的个数有x个.
![]() =
= ![]() ,
,
解得x=1.
答:绿球的个数为1个
(2)解:共有12种情况,一绿一黄的情况有2种,小明赢的概率是 ![]() =
= ![]() ;一红一黄的情况有4种情况,那么小刚赢的概率是
;一红一黄的情况有4种情况,那么小刚赢的概率是 ![]() =
= ![]() ;所以游戏不公平;胜负规则为:摸出“一绿一黄”的情况小明赢;摸出“两红”的情况小刚赢.
;所以游戏不公平;胜负规则为:摸出“一绿一黄”的情况小明赢;摸出“两红”的情况小刚赢.

【解析】(1)等量关系为:绿球的个数占球的总个数的多少= ![]() ;(2)找到一绿一黄的情况占总情况的多少求得小明赢的概率,同理求得小刚赢的概率,看是否相同即可;修改的标准是两人赢的概率相同.
;(2)找到一绿一黄的情况占总情况的多少求得小明赢的概率,同理求得小刚赢的概率,看是否相同即可;修改的标准是两人赢的概率相同.
【考点精析】根据题目的已知条件,利用列表法与树状图法和概率公式的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.
-
科目: 来源: 题型:
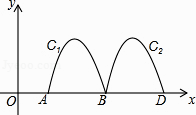
查看答案和解析>>【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A.﹣2<m<
B.﹣3<m<﹣
C.﹣3<m<﹣2
D.﹣3<m<﹣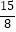
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形ABC中,AB=AC,∠B=30°,BC=
 cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.
cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.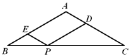
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 ﹣(﹣1)2015×(﹣
﹣(﹣1)2015×(﹣  )﹣2﹣|1﹣
)﹣2﹣|1﹣ 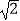 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
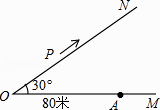
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距216千米,甲、乙分别在A、B两地,若甲骑车的速度为15千米/时,乙骑车的速度为12千米/时。.
(1)甲、乙同时出发,背向而行,问几小时后他们相距351千米?
(2)甲、乙相向而行,甲出发三小时后乙才出发,问乙出发几小时后两人相遇?
(3)甲、乙相向而行,要使他们相遇于AB的中点,乙要比甲先出发几小时?
(4)甲、乙同时出发,相向而行,甲到达B处,乙到达A处都分别立即返回,几小时后相遇?相遇地点距离A有多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
相关试题

