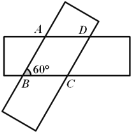
【题目】如图,将两条宽度为3的直尺重叠在一起,使∠ABC=60°,则四边形ABCD的面积是_____________
参考答案:
【答案】6![]()
【解析】先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形;根据宽度是3与∠ABC=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是3,
∴S四边形ABCD=AB×3=BC×3,
∴AB=BC,
∴平行四边形ABCD是菱形,即四边形ABCD是菱形.
如图,过A作AE⊥BC,垂足为E,
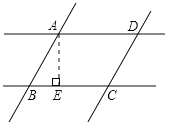
∵∠ABC=60,
∴∠BAE=90°60°=30°,
∴AB=2BE,
在△ABE中,AB2=BE2+AE2,
即AB2=![]() AB2+32,
AB2+32,
解得AB=![]() ,
,
∴S四边形ABCD=BCAE=![]() ×3=
×3=![]() .
.
故答案是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE . 现给出下列命题:
(i)若 =
= 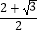 ,则tan∠EDF=
,则tan∠EDF= 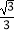
(ii)若DE2=BDEF,则DF=2AD
那么,下面判断正确的是( )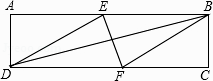
A.①正确,②正确
B.①正确,②错误
C.①错误,②正确
D.①错误,②错误 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数
 与方差s2如下表所示:
与方差s2如下表所示:甲
乙
丙
丁
平均数
 (cm)
(cm)561
560
561
560
方差s2
3.5
3.5
15.5
16.5
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁
-
科目: 来源: 题型:
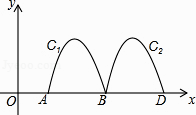
查看答案和解析>>【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A.﹣2<m<
B.﹣3<m<﹣
C.﹣3<m<﹣2
D.﹣3<m<﹣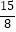
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰三角形ABC中,AB=AC,∠B=30°,BC=
 cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.
cm,P是BC上任意一点,过P作PD//AB,PE//AC,则PE+PD的值为__________________.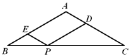
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 ﹣(﹣1)2015×(﹣
﹣(﹣1)2015×(﹣  )﹣2﹣|1﹣
)﹣2﹣|1﹣ 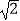 |
|
相关试题

