【题目】如图,高铁列车座位后面的小桌板收起时可以近似地看作与地面垂直,展开小桌板后,桌面会保持水平,其中图1、图2分别是小桌板收起时和展开时的实物,图3中的实线是小桌板展开后的示意图,其中OB表示小桌板桌面的宽度,BC表示小桌板的支架,连接OA,此时OA=75厘米,∠AOB=∠ACB=37°,且支架长BC与桌面宽OB的长度之和等于OA的长度,求点B到AC的距离.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)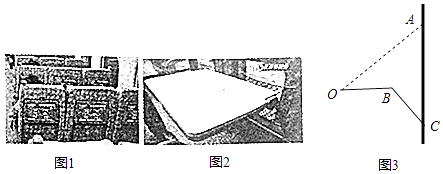
参考答案:
【答案】解:延长OB交AC于点D,
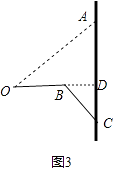
由题可知:BD⊥CA,
设BC=xcm,则BO=OA﹣BC=(75﹣x)cm,
在Rt△CBD中,
∵BD=BCsin∠ACB=xsin37°=0.6x,
∴DO=OB+BD=75﹣x+0.6x=(75﹣0.4x)cm,
在Rt△AOD中,
DO=AOcos∠AOD=75cos37°=60cm,
∴75﹣0.4x=60,
解得:x=37.5,
∴BD=0.6x=22.5cm,
答:点B到AC的距离为22.5cm.
【解析】根据已知条件,将实际问题转化为数学问题,画出图形,延长OB交AC于点D,利用解直角三角形的知识,在Rt△CBD中,用含x的式子分别表示出BD、DO的长,在Rt△AOD中,建立方程,求出x的值,就可求得BD的长。
【考点精析】本题主要考查了解直角三角形的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形的两边长,且k=4,求该矩形的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,添加以下条件,不能判定
,添加以下条件,不能判定 的是( )
的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区积极创建环保示范社区,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,已知温馨提示牌的单价为每个30元,垃圾箱的单价为每个90元,共需购买温馨提示牌和垃圾箱共100个.
(1)若规定温馨提示牌和垃圾箱的个数之比为1:4,求所需的购买费用;
(2)若该小区至多安放48个温馨提示牌,且费用不超过6300元,请列举所有购买方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买A、B两种道具.已知购买1件A道具比购买1件B道具多10元,购买2件A道具和3件B道具共需要45元.
(1)购买一件A道具和一件B道具各需要多少元?
(2)根据班级情况,需要这两种道具共60件,且购买两种道具的总费用不超过620元.
①请问道具A最多购买多少件?
②若其中A道具购买的件数不少于B道具购买件数,该班级共有几种方案?试写出所有方案,并求出最少费用为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.
如:①用配方法分解因式:a2+6a+8,
解:原式=a2+6a+8+1-1=a2+6a+9-1
=(a+3)2-12=

②M=a2-2a-1,利用配方法求M的最小值.
解:
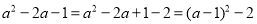
∵(a-b)2≥0,∴当a=1时,M有最小值-2.
请根据上述材料解决下列问题:
(1)用配方法因式分解:
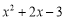 .
.(2)若
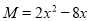 ,求M的最小值.
,求M的最小值.(3)已知x2+2y2+z2-2xy-2y-4z+5=0,求x+y+z的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将直角三角形 ABC 沿 AB 方向平移 AD 的长度得到三角形DEF,已知BE=5, EF=8, CG=2,则图中阴影部分的面积为__________.
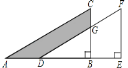
相关试题

