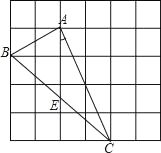
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
参考答案:
【答案】(1)作图见解析;(2)![]() ;(3)∠CAD;
;(3)∠CAD;![]() ;或∠ADC,
;或∠ADC,![]() .
.
【解析】试题分析:(1)直接利用网格结合平行线的判定方法得出D点位置;
(2)直接利用勾股定理得出DC的长;
(3)利用勾股定理的逆定理得出△ACD是直角三角形,进而得出答案;
(4)根据直角三角形斜边上的中线等于斜边的一半得出AE=EC,可得∠ACB=∠CAE,然后在Rt△ABC中求出tan∠ACB的值即为tan∠CAE的值.
试题解析:
解:(1)如图所示:
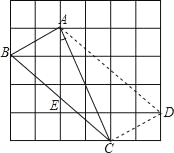
D点即为所求;
(2)DC=![]() =
=![]() ;
;
故答案为:![]() ;
;
(3)在△ACD的三个内角中所选的锐角是:∠CAD,
∵CD=![]() ,AD=5,AC=
,AD=5,AC=![]() ,
,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴∠CAD它所对应的正弦函数值是:![]() =
=![]() ;
;
当所选的锐角是:∠ADC,
则∠ADC它所对应的正弦函数值是:![]() =
=![]() .
.
故答案为:∠CAD,![]() 或∠ADC,
或∠ADC,![]() ;
;
(4)AB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
∵E为BC中点,
∴AE=EC,
∴∠ACB=∠CAE,
∴tan∠CAE=tan∠ACB=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
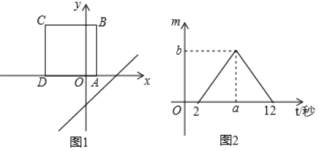
A. 5
 B. 4
B. 4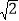 C. 3
C. 3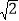 D. 2
D. 2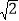
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3、﹣2、﹣1、1、2、3六个数中任选一个数记为k,若数k使得关于x的分式方程
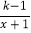 =k﹣2有解,且使关于x的一次函数y=(k+
=k﹣2有解,且使关于x的一次函数y=(k+ )x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )
)x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )A. ﹣1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

-
科目: 来源: 题型:
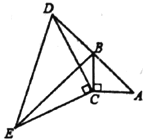
查看答案和解析>>【题目】如图,在
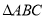 中,
中,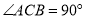 ,
,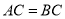 ,延长
,延长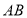 至点
至点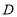 ,使
,使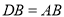 ,连接
,连接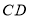 ,以
,以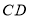 为直角边在
为直角边在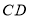 左侧作等腰三角形
左侧作等腰三角形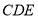 ,其中
,其中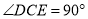 ,连接
,连接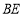 .
.
(1)求证:
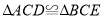 ;
;(2)若
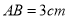 ,求
,求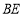 的长.
的长.(3)
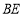 与
与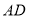 有何位置关系?请说明理由.
有何位置关系?请说明理由. -
科目: 来源: 题型:
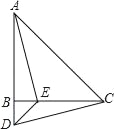
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠ACD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,点
,点 是射线
是射线 上一动点(与点
上一动点(与点 不重合),
不重合), 分别平分
分别平分 和
和 ,分别交射线
,分别交射线 于点
于点 .
.
(1)
 ;
; ;
;(2)当点
 运动到某处时,
运动到某处时, ,求此时
,求此时 的度数.
的度数.(3)当点
 运动时,
运动时, :
: 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
相关试题

