【题目】从﹣3、﹣2、﹣1、1、2、3六个数中任选一个数记为k,若数k使得关于x的分式方程![]() =k﹣2有解,且使关于x的一次函数y=(k+
=k﹣2有解,且使关于x的一次函数y=(k+![]() )x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )
)x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )
A. ﹣1B. 2C. 3D. 4
参考答案:
【答案】B
【解析】
首先利用一次函数的性质,求得当k=-1,1,2,3时,关于x的一次函数y=(k+![]() )x+2不经过第四象限,再利用分式方程的知识求得当k=-1,3,使得关于x的分式方程
)x+2不经过第四象限,再利用分式方程的知识求得当k=-1,3,使得关于x的分式方程![]() =k-2有解,然后再把-1和3相加即可.
=k-2有解,然后再把-1和3相加即可.
解:∵关于x的一次函数y=(k+![]() )x+2不经过第四象限,
)x+2不经过第四象限,
∴k+![]() >0,
>0,
解得,k>﹣1.5,
∵关于x的分式方程![]() =k﹣2有解,
=k﹣2有解,
∴当k=﹣1时,分式方程![]() =k﹣2的解是x=
=k﹣2的解是x=![]() ,
,
当k=1时,分式方程![]() =k﹣2无解,
=k﹣2无解,
当k=2时,分式方程![]() =k﹣2无解,
=k﹣2无解,
当k=3时,分式方程![]() =k﹣2的解是x=1,
=k﹣2的解是x=1,
∴符合要求的k的值为﹣1和3,
∵﹣1+3=2,
∴所有满足条件的k的值之和是2,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
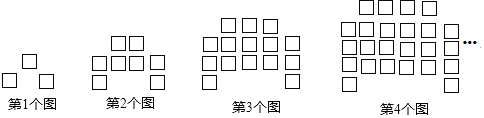
A. 48B. 63C. 80D. 99
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
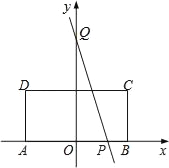
A.
 或-
或- B.
B.  或-
或- C.
C. 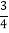 或-
或-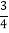 D.
D.  或-
或-
-
科目: 来源: 题型:
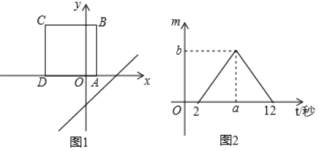
查看答案和解析>>【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
A. 5
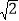 B. 4
B. 4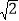 C. 3
C. 3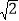 D. 2
D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

-
科目: 来源: 题型:
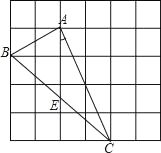
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
-
科目: 来源: 题型:
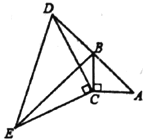
查看答案和解析>>【题目】如图,在
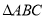 中,
中,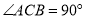 ,
,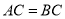 ,延长
,延长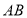 至点
至点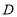 ,使
,使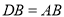 ,连接
,连接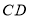 ,以
,以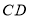 为直角边在
为直角边在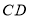 左侧作等腰三角形
左侧作等腰三角形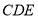 ,其中
,其中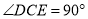 ,连接
,连接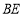 .
.
(1)求证:
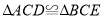 ;
;(2)若
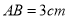 ,求
,求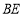 的长.
的长.(3)
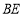 与
与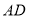 有何位置关系?请说明理由.
有何位置关系?请说明理由.
相关试题

