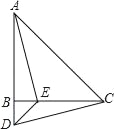
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为直角边在
为直角边在![]() 左侧作等腰三角形
左侧作等腰三角形![]() ,其中
,其中![]() ,连接
,连接![]() .
.
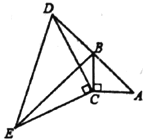
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
(3)![]() 与
与![]() 有何位置关系?请说明理由.
有何位置关系?请说明理由.
参考答案:
【答案】(1)见解析;(2)6cm;(3)![]() ,见解析.
,见解析.
【解析】
(1)根据等腰直角三角形的性质得到CD=CE,CA=CB,然后利用“SAS”可判断△ACD≌△BCE;
(2)根据全等三角形的性质得到AD=BE,而DB=AB=3cm,所以BE=6cm;
(3)根据全等三角形的性质得到∠1=∠2,而∠3=∠4,然后根据三角形内角和定理即可得到∠EBD=∠ECD=90°
(1)证明:∵![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
∵![]() .
.
∴![]() ;
;
(2)解:∵![]() ,
,![]()
∴![]() ,
,
∵![]() ;
;
∴![]() ,
,
即BE的长为![]() .
.
(3)![]() .
.
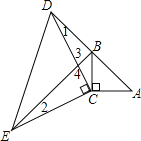
理由如下:
如图:
∵△ACD≌△BCE,
∴∠1=∠2,
而∠3=∠4,
∴∠EBD=∠ECD=90°,
∴BE⊥AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3、﹣2、﹣1、1、2、3六个数中任选一个数记为k,若数k使得关于x的分式方程
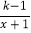 =k﹣2有解,且使关于x的一次函数y=(k+
=k﹣2有解,且使关于x的一次函数y=(k+ )x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )
)x+2不经过第四象限,那么这6个数中,所有满足条件的k的值之和是( )A. ﹣1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

-
科目: 来源: 题型:
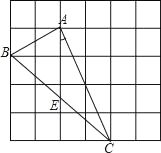
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠ACD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,点
,点 是射线
是射线 上一动点(与点
上一动点(与点 不重合),
不重合), 分别平分
分别平分 和
和 ,分别交射线
,分别交射线 于点
于点 .
.
(1)
 ;
; ;
;(2)当点
 运动到某处时,
运动到某处时, ,求此时
,求此时 的度数.
的度数.(3)当点
 运动时,
运动时, :
: 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律; -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.

(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 平均数是 中位数为
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
相关试题

