【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠ABC的平分线BE交⊙O于点E,∠ACB的平分线CF交⊙O于点F,BE和CF相交于点D,四边形AFDE是菱形吗?请证明你的结论.

参考答案:
【答案】四边形AFDE是菱形.证明见解析.
【解析】试题分析:由AB=AC,BE平分∠ABC,CF平分∠ACB,可证∠ABE=∠EBC=∠ACF=∠FCB,再由圆周角定理的推论可证∠FAB=∠ABE=∠EAC=∠ACF.从而可证四边形AFDE是平行四边形,再证AF=AE,即证四边形AFDE是菱形.
解:四边形AFDE是菱形.
证明:∵AB=AC,
∴∠ABC=∠ACB.
又∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠EBC=∠ACF=∠FCB.
∵∠FAB,∠FCB是同弧所对的圆周角,
∴∠FAB=∠FCB,
同理∠EAC=∠EBC.
∴∠FAB=∠ABE=∠EAC=∠ACF.
∴AF∥ED,AE∥FD,
∴四边形AFDE是平行四边形.
∵∠ABE=∠ACF,
∴![]() =
=![]() ,
,
∴AF=AE.
∴四边形AFDE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D.已知OA=OB=6 cm,AB=6
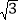 cm.
cm.(1)求⊙O的半径;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
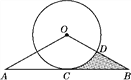
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边上一点,DE⊥AB,且DE=AC,DE与AC交于点G,过点E作FE∥BC交AB于点F,交AC于点H.
(1)求证:△ABC≌△EFD;
(2)若∠EFD=55°,求∠DGH的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知: A 0,1 , B 2, 0 , C 4, 3 .
(1)求△ABC 的面积;
(2)设点 P 在坐标轴上,且△ABC 和△ABP 的面积相等,直接写出 P 的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门).安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是
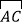 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.(1)求证:△PAC∽△PDF;
(2)若AB=5,
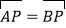 ,求PD的长;
,求PD的长;(3)在点P运动过程中,设
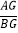 =x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)
=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)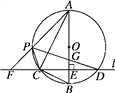
-
科目: 来源: 题型:
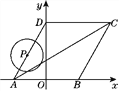
查看答案和解析>>【题目】如图,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
(1)求线段AD所在直线的表达式;
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
相关试题

