【题目】阅读材料:对于一个关于![]() 的一元二次方程
的一元二次方程![]() (其中a≠0,a、b、c为常数)的两根分别为
(其中a≠0,a、b、c为常数)的两根分别为![]() ,
,![]() ,我们有如下发现①若
,我们有如下发现①若![]() ,
,![]() 为整数,则这个一元二次方程的判别式
为整数,则这个一元二次方程的判别式![]() 一定为完全平方数;②
一定为完全平方数;② ![]() ,
,![]() 满足韦达定理:即
满足韦达定理:即![]() ,
,![]() ;
;
③韦达定理也有逆定理,即如果两数![]() 和
和![]() 满足如下关系:
满足如下关系:![]() ,
,![]() ,那么这两个数
,那么这两个数![]() 和
和![]() 是方程
是方程![]() (
(![]() )的两个根.
)的两个根.
请应用上述材料解决以下问题:
(1)若实数![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,
的两个根,
①当![]() 时,则
时,则![]() ,
,![]() ;
;
②若![]() 均为整数且
均为整数且![]() ,求
,求![]() 的值;
的值;
(2)已知实数![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)①-1,-8;②![]() ;(2)71.
;(2)71.
【解析】
(1)①利用根与系数的关系求解即可;
②根据所给材料可知![]() 为完全平方数,结合
为完全平方数,结合![]() 可求出m=13;
可求出m=13;
(2)利用已知得出xy,x+y看作一元二次方程![]() 的两个实数根,进而得出答案.
的两个实数根,进而得出答案.
(1).① -1 , -8
②∵![]() 为整数
为整数
∴上材料可知![]() 为完全平方数
为完全平方数
即![]() 为完全平方数
为完全平方数
∵![]() 是整数,且
是整数,且![]()
∴只有当![]() 时满足条件.
时满足条件.
(2)∵![]()
∴![]()
又∵![]()
∴![]() 和
和![]() 可以看成是方程
可以看成是方程![]() 的两个根.
的两个根.
∴![]()
∴![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年暑假都是旅游旺季,某商家抓住商机,准备七、八月份力推A、B两款旅行箱,已知7月份销售10件A款旅行箱和20件B款旅行箱的总销售额为4800元,每件B款旅行箱比每件A款旅行箱的销售单价多60元。该商家在七月份A、B两款旅行箱都卖了200件.
(1)求A、B两款旅行箱的销售单价分别为多少元?
(2)八月份,A款旅行箱的销售单价在七月份的基础上上涨了0.5a%,B款旅行箱的销售单价在七月份的基础上上涨了a%,两款旅行箱的销售量都比七月份减少了
 a%,该商家发现两款旅行箱八月份的总销售额比七月份的总销售额少3000元,求a的值.
a%,该商家发现两款旅行箱八月份的总销售额比七月份的总销售额少3000元,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平形行四边形ABCD中,连接对角线BD,AB=BD,E为线段AD上一点,AE=BE
(1)如图1,若∠ABE=30,CD=
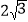 ,求DE的长;
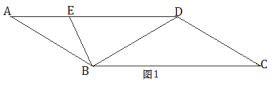
,求DE的长;(2)如图2,F为线段BE上一点,DE=BF,连接AF、DF,DF的延长线交AB于点G,若AF=2DE,求证:DF=2GF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.
例如计算:(2-i)+(5+3i)=(2+5)+(-1+3)i=7+2i;
(1+i)×(2-i)=1×2-i+2×i-i2=2+(-1+2)i+1=3+i;
根据以上信息,完成下列问题:
(1)填空:i3= ,i4= ;
(2)计算:(1+i)×(3-4i);
(3)计算:i+i2+i3+…+i2018.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某项研究表明,大拇指与小拇指尽量张开时,两指尖的距离称为指距.如表是测得的指距与身高的一组数据:
指距d(cm)
19
20
21
身高h(cm)
151
160
169
(1)你能确定身高h与指距d之间的函数关系式吗?
(2)若某人的身高为196cm,一般情况下他的指距应是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=
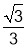 x2﹣
x2﹣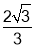 x﹣
x﹣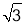 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.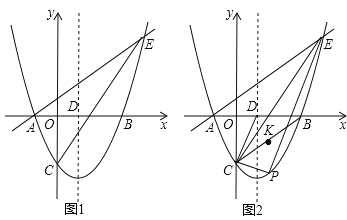
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=
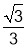 x2﹣
x2﹣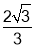 x﹣
x﹣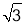 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,且BC=2AF。
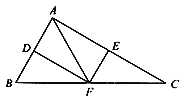
(1)求证:四边形ADEF为矩形;
(2)若∠C=30°、AF=2,写出矩形ADEF的周长。
相关试题

