【题目】如图,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x+
x+![]() .(2)3,(3)点Q的坐标为(3,
.(2)3,(3)点Q的坐标为(3,![]() ),Q′(3,
),Q′(3,![]() )或(3,2
)或(3,2![]() )或(3,﹣
)或(3,﹣![]() ).
).
【解析】
试题分析:(1)抛物线的解析式可以变天为y=![]() (x+1)(x-3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入,求得k和b的值,从而得到AE的解析式;
(x+1)(x-3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入,求得k和b的值,从而得到AE的解析式;
(2)设直线CE的解析式为y=mx-![]() ,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE于点F,设点P的坐标为(x,
,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE于点F,设点P的坐标为(x,![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ),则点F(x,
),则点F(x,![]() x-
x-![]() ),则FP=﹣
),则FP=﹣![]() x2+
x2+![]() .由三角形的面积公式得:ΔEPC的面积=-
.由三角形的面积公式得:ΔEPC的面积=-![]() x2+
x2+![]() x,利用二次函数的媒体人富士康得x的值,从而求得点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP于N、M,然后利用轴对称的性质可得到点G和H的坐标,当点O、N、M、H在一条直线上时,KM+MN+NK有最小值,最小值=GH。
x,利用二次函数的媒体人富士康得x的值,从而求得点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP于N、M,然后利用轴对称的性质可得到点G和H的坐标,当点O、N、M、H在一条直线上时,KM+MN+NK有最小值,最小值=GH。
(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为QG=FG、QG=QF、FQ=FQ三种情况求解即可.
试题解析:(1)∵y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ,
,
∴y=![]() (x+1)(x﹣3).
(x+1)(x﹣3).
∴A(﹣1,0),B(3,0).
当x=4时,y=![]() .
.
∴E(4,![]() ).
).
设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得:
 ,
,
解得:k=![]() ,b=
,b=![]() .
.
∴直线AE的解析式为y=![]() x+
x+![]() .
.
(2)设直线CE的解析式为y=mx﹣![]() ,将点E的坐标代入得:4m﹣
,将点E的坐标代入得:4m﹣![]() =
=![]() ,解得:m=
,解得:m=![]() .
.
∴直线CE的解析式为y=![]() x﹣
x﹣![]() .
.
过点P作PF∥y轴,交CE与点F.
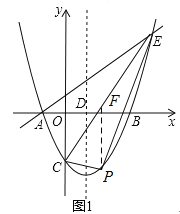
设点P的坐标为(x,![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ),则点F(x,
),则点F(x,![]() x﹣
x﹣![]() ),
),
则FP=(![]() x﹣
x﹣![]() )﹣(
)﹣(![]() x2﹣
x2﹣![]() x﹣
x﹣![]() )=
)=![]() x2+
x2+![]() x.
x.
∴△EPC的面积=![]() ×(
×(![]() x2+
x2+![]() x)×4=﹣
x)×4=﹣![]() x2+
x2+![]() x.
x.
∴当x=2时,△EPC的面积最大.
∴P(2,﹣![]() ).
).
如图2所示:作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.
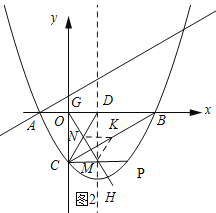
∵K是CB的中点,
∴k(![]() ,﹣
,﹣![]() ).
).
∵点H与点K关于CP对称,
∴点H的坐标为(![]() ,﹣
,﹣![]() ).
).
∵点G与点K关于CD对称,
∴点G(0,0).
∴KM+MN+NK=MH+MN+GN.
当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.
∴GH=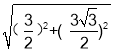 =3.
=3.
∴KM+MN+NK的最小值为3.
(3)如图3所示:

∵y′经过点D,y′的顶点为点F,
∴点F(3,﹣![]() ).
).
∵点G为CE的中点,
∴G(2,![]() ).
).
∴FG= .
.
∴当FG=FQ时,点Q(3,![]() ),Q′(3,
),Q′(3,![]() ).
).
当GF=GQ时,点F与点Q″关于y=![]() 对称,
对称,
∴点Q″(3,2![]() ).
).
当QG=QF时,设点Q1的坐标为(3,a).
由两点间的距离公式可知:a+![]() =
= ,解得:a=﹣
,解得:a=﹣![]() .
.
∴点Q1的坐标为(3,﹣![]() ).
).
综上所述,点Q的坐标为(3,![]() ),Q′(3,
),Q′(3,![]() )或(3,2
)或(3,2![]() )或(3,﹣
)或(3,﹣![]() ).
).
-
科目: 来源: 题型:
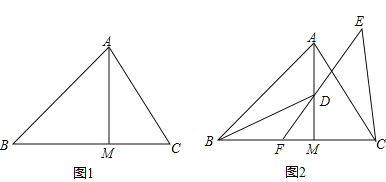
查看答案和解析>>【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图1,若AB=3
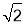 ,BC=5,求AC的长;
,BC=5,求AC的长;(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点E,F分别为ABCD的边BC,AD上的点,且∠1=∠2.
求证:AE=CF.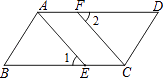
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
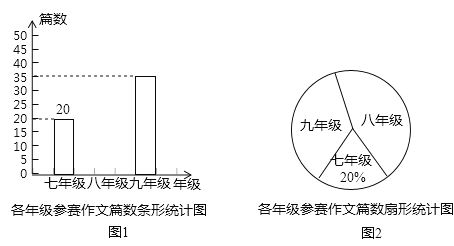
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年,安徽省财政总收入为4373亿元,比上年增加9%,其中“4373亿”这个数据用科学记数法表示是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解;
(1)2a2﹣2;
(2)m2﹣12mn+36n2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:
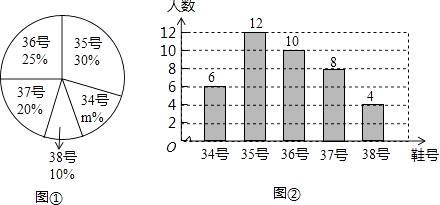
(1)本次接受随机抽样调查的学生人数为 , 图①中m的值为;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?
相关试题

