【题目】如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,以下四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC,其中一定正确的是_____.

参考答案:
【答案】③④
【解析】
由旋转的性质可得AC=CD,BC=CE,AB=DE,可判断①③,等腰三角形的性质可判断④,由于∠A+∠ABC不一定等于90°,于是得到∠ABC+∠CBE不一定等于90°,故②错误.
解:∵将△ABC绕点C顺时针旋转得到△DEC,
∴AC=CD,BC=CE,AB=DE,故①错误,③正确;
∴∠ACD=∠BCE,
∴∠A=∠ADC=![]() (180°﹣∠ACD),∠CBE=
(180°﹣∠ACD),∠CBE=![]() (180°﹣∠BCE),
(180°﹣∠BCE),
∴∠A=∠EBC,故④正确;
∵∠A+∠ABC不一定等于90°,
∴∠ABC+∠CBE不一定等于90°,故②错误;
故答案为:③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为( )

A. 3 B. 2 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名同学调查了全班
 名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:最喜欢的节目类别
划记
人数
百分数(%)
相声
正

小品
正正正一


歌曲
正正


舞蹈
正一

其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.相声B.小品C.歌曲D.舞蹈
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若
 ,则
,则 =( )
=( )
A. 6 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
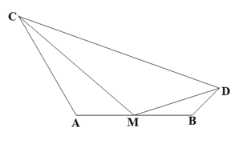
查看答案和解析>>【题目】如图,AC,BD在AB的同侧,AC=10,BD=3,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山东省泰安市)某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)

根据图表提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为400人
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中喜欢选修课E、F的人数分别为80,70
D. 喜欢选修课C的人数最少
-
科目: 来源: 题型:
查看答案和解析>>【题目】有五张正面分别标有数字﹣2,﹣1,0,1,2的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,0)的概率是__.
相关试题

