【题目】如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点. 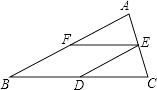
(1)求证:四边形BDEF是菱形;
(2)若AB=12cm,求菱形BDEF的周长.
参考答案:
【答案】
(1)证明:∵D、E、F分别是BC、AC、AB的中点,
∴DE∥AB,EF∥BC,
∴四边形BDEF是平行四边形,
又∵DE= ![]() AB,EF=
AB,EF= ![]() BC,且AB=BC,
BC,且AB=BC,
∴DE=EF,
∴四边形BDEF是菱形
(2)解:∵AB=12cm,F为AB中点,
∴BF=6cm,
∴菱形BDEF的周长为6×4=24cm
【解析】(1)可根据菱形的定义“一组邻边相等的平行四边形是菱形”,先证明四边形BFED是平行四边形,然后再证明四边形的邻边相等即可.(2)F是AB的中点,有了AB的长也就求出了菱形的边长BF的长,那么菱形BDEF的周长也就能求出了.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一元二次方程3x2﹣2x=1化成一般形式后,二次项系数和常数项分别是( )
A. 3、1B. 3、2C. 3、﹣1D. 3、﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
①AD=BC;②BD、AC互相平分;③四边形ACED是菱形;④BD⊥DE.
其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,三个内角的平分线交于点O,过点O作OD⊥OB,交边BC于点D.
(1)如图1,猜想∠AOC与∠ODC的关系,并说明你的理由;
(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F. ①求证:BF∥OD;
②若∠F=35°,求∠BAC的度数.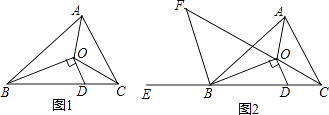
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.
(1)若∠ACB=∠CDB=90°,求证:∠CFE=∠CEF;
(2)若∠ACB=∠CDB=m(0°<m<180°). ①求∠CEF﹣∠CFE的值(用含m的代数式表示);
②是否存在m,使∠CEF小于∠CFE,如果存在,求出m的范围,如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(﹣4,2)关于原点对称的点的坐标为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )

A.40°
B.45°
C.50°
D.55°
相关试题

