Question

【题目】若a、b满足，且A(a，0)、B(0，b)

(1) 如图，在x正半轴上有一点C（x，0）．若△ABC的面积大于6，请直接写出x的取值范围____________；

(2)若在平面直角坐标系第四象限上存在一点N，N的坐标为(n，﹣n)，满足4≤S△ABN≤8，求n的取值范围．

(3)若在平面直角坐标系上存在一点M，M的坐标为(m，﹣2m)，请通过计算说明：无论m取何值△ABM的面积为定值，并求出这个值．

Answer 1

【答案】(1)；(2) (3) 无论m取何值△ABM的面积为定值，面积为1个单位平方，证明见解析．

【解析】

（1）根据非负数的性质求出a，b的值，得到A，B点的坐标，根据三角形面积公式列出不等式求解即可；

（2）分N点在直线AB左侧时（n＞0）和右侧时（n＞0）两种情况求解，分别求出S△ABN用n表示的代数式，再解不等式组即可；

（3）分三种情况，根据三角形面积计算公式进行求解即可．

(1) ∵

∴

解得，

∴A（1，0），B（0，2）

∴OA=1，OB=2，

∵C（x，0）

∴AC=x-1

∴S△ABC=

解得，，

故答案为：；

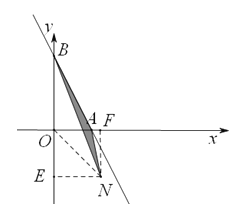
(2)当N点在直线AB左侧时（n＞0）

过N做NF⊥x轴于F，做NE⊥y轴于E，

∵N(n，﹣n)，A(1，0)，B(0，2)，

∴AO=1，BO=2，EN=FN=n

∴S△ABN=S△AON+S△ABO﹣S△OBN

∴S△ABN=

∴ ∴,不合题意舍去;

当N点在直线AB右侧时（n＞0）

过N做NF⊥x轴于F，做NE⊥y轴于E，

∵N(n，﹣n)，A(1，0)，B(0，2)，

∴AO=1，BO=2，EN=FN=n

∴S△ABN=S△BON﹣S△ABO﹣S△AON

∴S△ABN=

∴ ∴

综上所述：n的取值范围为

(3)证明：1)当点M为原点（m=0）时， S△ABM=1

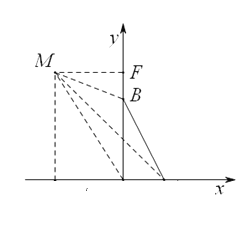
2)当点M（m＜0）在第二象限时，如图：

过M做ME⊥x轴于E，做MF⊥y轴于F

∵M(m，﹣2m)，A(1，0)，B(0，2)，

∴MF=﹣m，EM=﹣2m，AO=1，BO=2,

∴S△ABM=S△BOM+S△ABO﹣S△OAM

∴S△ABM=

∴S△ABM=1

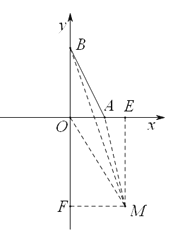
3)当点M（m＞0）在第四象限时，如图：

过M做EF⊥x轴于F，过B点做BE⊥EF于E

∵M(m，﹣2m)，A(1，0)，B(0，2)，

∴MF=m，EM=2m，AO=1，BO=2,

∴S△ABM=S△AOM+S△ABO﹣S△BOM

∴S△ABM=

∴S△ABM=1

综上所述：无论m取何值△ABM的面积为定值，面积为1个单位平方．