【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD之间的位置关系为 , 数量关系为 .
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,为什么?
(2)如图4,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且AC=4 ![]() ,BC=3,∠BCA=45°,正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,∠BCA=45°,正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
参考答案:
【答案】
(1)CF⊥BD,CF=BD,解:成立,理由如下:∵∠FAD=∠BAC=90°,∴∠BAD=∠CAF在△BAD与△CAF中, .∴△BAD≌△CAF,∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°∴CF⊥BD;
.∴△BAD≌△CAF,∴CF=BD,∠ACF=∠ACB=45°,∴∠BCF=90°∴CF⊥BD;
(2)解:如图,过点A作AG⊥AC交CB的延长线于点G,
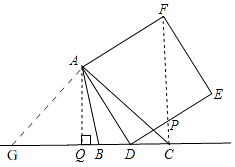
则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°﹣∠ACB,
∴∠AGC=90°﹣45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
在△GAD与△CAF中, 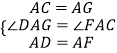 ,
,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∠BCF=∠ACB+∠ACF=45°+45°=90°,
即CF⊥BC.
过点A作AQ⊥BC交CB的延长线于点Q,
∵DE与CF交于点P时,此时点D位于线段CQ上,
∵∠BCA=45°,AC=4 ![]() ,
,
∴由勾股定理得AQ=CQ=4.
设CD=x,
∴DQ=4﹣x,
∵∠ADB+∠ADE+∠PDC=180°
且∠ADE=90°,
∴∠ADQ+∠PDC=90°,
又∵在Rt△PCD中,∠PDC+∠DPC=90°
∴∠ADQ=∠DPC,
∵∠AQD=∠DCP=90°
∴△AQD∽△DCP,
∴ ![]() ,
,
∴ ![]() .
.
∴CP=﹣ ![]() x2+x=﹣
x2+x=﹣ ![]() (x﹣2)2+1.
(x﹣2)2+1.
∴当x=2时,CP有最大值1.
【解析】解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中, 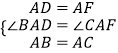 ,
,
∴△DAB≌△FAC,
∴CF=BD,∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
所以答案是:CF⊥BD,CF=BD;
【考点精析】关于本题考查的勾股定理的概念和正方形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究:
如图,抛物线y= x2﹣
x2﹣  x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b满足,
 且A(a,0)、B(0,b)
且A(a,0)、B(0,b)
(1) 如图,在x正半轴上有一点C(x,0).若△ABC的面积大于6,请直接写出x的取值范围____________;
(2)若在平面直角坐标系第四象限上存在一点N,N的坐标为(n,﹣n),满足4≤S△ABN≤8,求n的取值范围.
(3)若在平面直角坐标系上存在一点M,M的坐标为(m,﹣2m),请通过计算说明:无论m取何值△ABM的面积为定值,并求出这个值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,
 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论 ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:小青:
 ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;小夏:
 ;小雨:
;小雨: .
.这四位同学写出的结论中不正确的是



A. 小青 B. 小何 C. 小夏 D. 小雨
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥ED,CD=BF,若要说明△ABC ≌△EDF,则不能补充的条件是( )

A.AC=EFB.AB=EDC.∠A=∠ED.AC∥EF
-
科目: 来源: 题型:
查看答案和解析>>【题目】五一小长假的某一天,亮亮全家上午
 时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
时自驾小汽车从家里出发,到某旅游景点游玩,该小汽车离家的距离(千米)与时间(时)之间的关系如图所示,根据图像提供的有关信息,判断下列说法错误的是( )
A.景点离亮亮的家
 千米
千米B.亮亮到家的时间为
 时
时C.小汽车返程的速度为
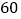 千米/时
千米/时D.
 时至
时至 时,小汽车匀速行驶
时,小汽车匀速行驶 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,将Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角最小为( )

A.115°
B.125°
C.120°
D.145°
相关试题

