【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,![]() 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论![]() ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:
小青:![]() ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;
小夏:![]() ;小雨:
;小雨:![]() .
.
这四位同学写出的结论中不正确的是![]()
![]()

A. 小青 B. 小何 C. 小夏 D. 小雨
参考答案:
【答案】B
【解析】
利用平行四边形的性质、全等三角形的判定和性质,一一判断即可.
∵四边形ABCD是平行四边形,
∴OA=OC,CD∥AB,
∴∠ECO=∠FAO,(故小雨的结论正确),
在△EOC和△FOA中,

∴△EOC≌△FOA,
∴OE=OF(故小青的结论正确),
∴S△EOC=S△AOF,
∴S四边形AFED=S△ADC=![]() S平行四边形ABCD,
S平行四边形ABCD,
∴S四边形AFED=S四边形FBCE故小夏的结论正确,
∵△EOC≌△FOA,
∴EC=AF,∵CD=AB,
∴DE=FB,DE∥FB,
∴四边形DFBE是平行四边形,
∵OD=OB,EO⊥DB,
∴ED=EB,
∴四边形DFBE是菱形,无法判断是正方形,故小何的结论错误,

故选:B
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30
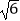 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积. -
科目: 来源: 题型:
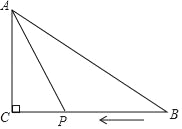
查看答案和解析>>【题目】如图,在三角形ABC中,∠C=90°,AC=6cm,BC=10cm,点P从B点开始向C点运动速度是每秒1cm,设运动时间是t秒,
(1)用含t的代数式来表示三角形ACP的面积.
(2)当三角形ACP的面积是三角形ABC的面积的一半时,求t的值,并指出此时点P在BC上的什么位置?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用白铁皮做罐头盒,每张铁皮可做盒身25个,或做盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?
①设用x张制盒身,可得方程2×25x=40(36﹣x);
②设用x张制盒身,可得方程25x=2×40(36﹣x);
③设用x张制盒身,y张制盒底,可得方程组
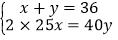 ;
;④设用x张制盒身,y张制盒底,可得方程组
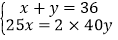 ;其中正确的是( )
;其中正确的是( )A. ①④ B. ②③ C. ②④ D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
 AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
A. ①② B. ②③ C. ①③ D. ①④
相关试题

