【题目】如图,已知AB是⊙O的直径,BC是弦,∠ABC=30°,过圆心O作OD⊥BC,垂足为E,交弧BC于点D,连接DC,则∠DCB的度数为( )

A. 30° B. 45° C. 50° D. 60°
参考答案:
【答案】A
【解析】
根据已知条件“过圆心O作OD⊥BC交弧BC于点D、,∠ABC=30°”、及直角三角形OBE的两个锐角互余求得∠BOE=60°;然后根据同弧BD所对的圆周角∠DCB是所对的圆心角∠DOB的一半,求得∠DCB的度数.
如图,
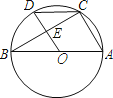
∵OD⊥BC,∠ABC=30°,
∴在直角三角形OBE中,
∠BOE=60°(直角三角形的两个锐角互余);
又∵∠DCB=![]() ∠DOB(同弧所对的圆周角是所对的圆心角的一半),
∠DOB(同弧所对的圆周角是所对的圆心角的一半),
∴∠DCB=30°;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
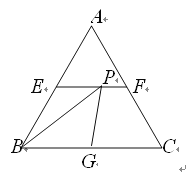
查看答案和解析>>【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、
AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是
_ ▲ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
 +px+q=0的两个根是
+px+q=0的两个根是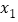 ,
,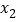 ,那么
,那么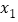 +
+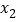 =-p,
=-p,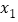
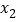 =q,反过来,如果
=q,反过来,如果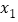 +
+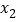 =-p,
=-p,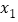
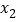 =q,那么以
=q,那么以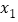 ,
,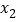 为两根的一元二次方程是
为两根的一元二次方程是 +px+q=0.请根据以上结论,解决下列问题:
+px+q=0.请根据以上结论,解决下列问题: (1)已知关于x的方程
 +mx+n=0(n≠0),求出—个一元二次方程,使它的两根分别是已知方程两根的倒数.
+mx+n=0(n≠0),求出—个一元二次方程,使它的两根分别是已知方程两根的倒数.(2)已知a、b满足
 -15a-5=0,
-15a-5=0, -15b-5=0,求
-15b-5=0,求 的值.
的值.(3)已知a、b、c均为实数,且a+b+c=0,abc=16,求正数c的最小值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AA1,A1A2,A2A3,A3B,AB分别是五个半圆的直径,两只小虫同时出发,以相同的速度从点A到点B,甲虫沿ADA1,A1EA2,A2FA3,A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )

A. 甲先到点B B. 乙先到点B C. 甲、乙同时到点B D. 无法确定谁先到点B
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是⊙O的直径,若∠A=10°,∠PMQ=40°,以PM为边作圆的内接正多边形,则这个正多边形是________边形.

相关试题

