【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

参考答案:
【答案】BM⊥BN.见解析
【解析】试题分析:根据SAS推出△ABE≌△DBC,推出AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,求出∠ABD=∠DBC=90°,BM=AM=EM=![]() AE,BN=CN=DN=
AE,BN=CN=DN=![]() CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
解:BM=BN,BM⊥BN,
理由是:在△ABE和△DBC中,
 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠DBC=90°,
∵M为AE的中点,N为CD的中点,
∴BM=AM=EM=![]() AE,BN=CN=DN=
AE,BN=CN=DN=![]() CD,
CD,
∴BM=BN,∠EAB=∠MBA,∠CDB=∠DBN,∠AEB=∠EBM,∠NCB=∠NBC,
∵∠EAB=∠BDC,∠AEB=∠DCB,
∴∠ABM=∠DBN,∠EBM=∠NBC,
∴∠ABC=2∠DBN+2∠EBM=180°,
∴∠EBN+∠EBM=90°,
∴BM⊥BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:(x2+x)2﹣8(x2+x)+12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若直线AB与直线CD交于点O,OA平分∠COF,OE⊥CD.
(1)写出图中与∠EOB互余的角;
(2)若∠AOF=30°,求∠BOE和∠DOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当x为何值时,代数式2(x+1)与代数式1﹣x的值互为相反数?
-
科目: 来源: 题型:
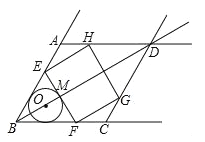
查看答案和解析>>【题目】(2016浙江省温州市第24题)如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6
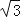 ,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.(1)求证:BO=2OM.
(2)设EF>HE,当矩形EFGH的面积为24
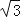 时,求⊙O的半径.
时,求⊙O的半径.(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随机从甲、乙两块试验田中各抽取100株麦苗测量高度,甲、乙两块试验田的平均数都是13,方差结果为:S甲2=36,S乙2=158,则小麦长势比较整齐的试验田是
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣3)+(﹣9)的结果是( )
A.+6
B.﹣6
C.﹣12
D.12
相关试题

