【题目】已知点A(1,2)、点 B在双曲线y= ![]() (x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,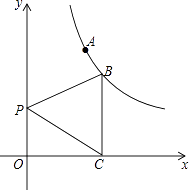
(1)求k的值及△PBC的面积;
(2)设点M(x1 , y1)、N(x2 , y2)(x2>x1>0)是双曲线y= ![]() (x>0)上的任意两点,s=
(x>0)上的任意两点,s= ![]() ,t=
,t= ![]() ,试判断s与t的大小关系,并说明理由.
,试判断s与t的大小关系,并说明理由.
参考答案:
【答案】
(1)解:把A(1,2)代入y= ![]() 得k=2;
得k=2;
设B的坐标是(m,n)则mn=2,BC=n,OC=m.
则S△PBC= ![]() BCOC=
BCOC= ![]() mn=1
mn=1
(2)解:s>t;
理由:∵s﹣t= ![]()
═ ![]()
═ ![]() =
= ![]() ,
,
∵x2>x1>0,
∴ ![]() >0,x1x2(x1+x2)>0,
>0,x1x2(x1+x2)>0,
∴ ![]() ;
;
∴s>t
【解析】(1)利用待定系数法即可求得k的值;设B的坐标是(m,n)则mn=2,BC=n,OC=m,利用三角形的面积公式求解;(2)把y1和y2用x1和x2,然后求s﹣t得值,对式子进行变形判断s﹣t的符号即可。
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份
一
二
三
四
用水量(吨)
16
18
30
35
水费(元)
32
36
65
80
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.
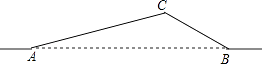
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”
 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:班级
一班
二班
三班
四班
五班
六班
人数
40
43
45
44
40
38
件数
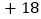
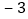
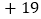
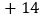
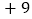
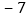
 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件? 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt△ABQ,使∠BAQ=90°,tan∠ABQ=
 ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=  CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.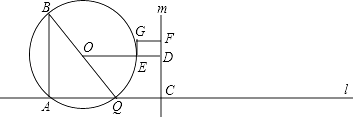
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求EE′的长?并求出∠BE′C的度数?
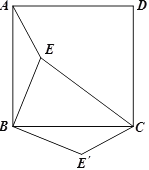
-
科目: 来源: 题型:
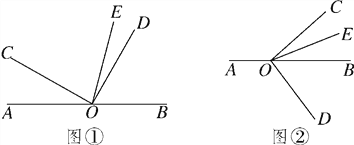
查看答案和解析>>【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
相关试题

