【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt△ABQ,使∠BAQ=90°,tan∠ABQ= ![]() ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.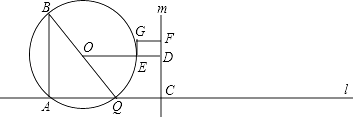
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值.
参考答案:
【答案】
(1)解:∵点Q沿着直线l以3厘米/秒的速度由点A向右运动,运动时间为t秒.
∴AQ=3t,
∵∠BAQ=90°,tan∠ABQ= ![]() =
= ![]() ,
,
∴AB=4t,
∴BQ= ![]() =5t,
=5t,
作OM⊥AQ于M,则AM=QM= ![]() AQ=1.5t,CD=OM,
AQ=1.5t,CD=OM,
∴OM是△ABQ的中位线,
∴CD=OM= ![]() AB=2t,
AB=2t,
∴DF= ![]() CD=
CD= ![]() t
t
(2)解:设矩形DEGF的面积为S,
∵OE=OB= ![]() BQ=
BQ= ![]() t,OD=QM+CQ=
t,OD=QM+CQ= ![]() t+1,
t+1,
∴DE=OD﹣OE= ![]() t+1﹣
t+1﹣ ![]() t=1﹣t,
t=1﹣t,
∴ ![]() ,
,
∴当t= ![]() 时,矩形DEGF的最大面积为
时,矩形DEGF的最大面积为 ![]()
(3)解:当矩形DEGF为正方形时,则DE=DF,分两种情况:
①当0<t<1时,如图1所示:
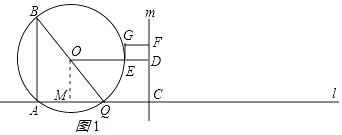
DE=1﹣t,
∴1﹣t= ![]() t,
t,
解得:t= ![]() ;
;
②当t≥1时,如图2所示:
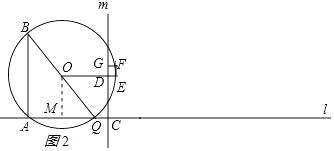
DE=t﹣1,
∴t﹣1= ![]() t,
t,
解得:t=3;
综上所述:当矩形DEGF为正方形时,t的值为 ![]() 或3.
或3.
【解析】(1)由已知得出AQ=3t,由三角函数求出AB=4t,再由勾股定理求出BQ= 5t,作OM⊥AQ于M,则AM=QM= ![]() AQ=1.5t,CD=OM,由三角形的中位线定理得出CD=OM=
AQ=1.5t,CD=OM,由三角形的中位线定理得出CD=OM= ![]() AB=2t,进而得出结论;
AB=2t,进而得出结论;
(2)设矩形DEGF的面积为S,OE= ![]() t,OD=QM+CQ=
t,OD=QM+CQ= ![]() t+1,
t+1,
∴DE=OD﹣OE= ![]() t+1﹣
t+1﹣ ![]() t=1﹣t,由矩形的面积得出s是t的二次函数,即可得出答案;
t=1﹣t,由矩形的面积得出s是t的二次函数,即可得出答案;
(3)当矩形DEGF为正方形时,则DE=DF,分两种情况:①当0<t<1时,如图1所示得出方程,解方程即可;②当t≥1时,如图2所示:DE=t﹣1,得出方程,解方程即可。
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A,B两地之间修建一条笔直的公路.
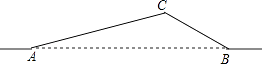
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”
 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:班级
一班
二班
三班
四班
五班
六班
人数
40
43
45
44
40
38
件数
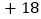
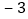
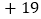
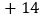
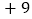
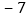
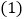 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?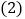 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,2)、点 B在双曲线y=
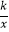 (x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,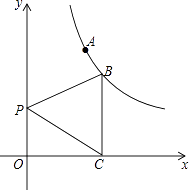
(1)求k的值及△PBC的面积;
(2)设点M(x1 , y1)、N(x2 , y2)(x2>x1>0)是双曲线y=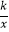 (x>0)上的任意两点,s=
(x>0)上的任意两点,s= 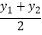 ,t=
,t= 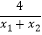 ,试判断s与t的大小关系,并说明理由.
,试判断s与t的大小关系,并说明理由. -
科目: 来源: 题型:
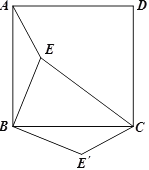
查看答案和解析>>【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求EE′的长?并求出∠BE′C的度数?
-
科目: 来源: 题型:
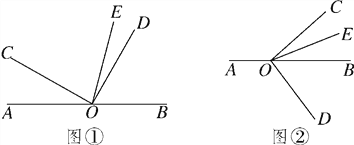
查看答案和解析>>【题目】(12分)已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置.
①探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
②在∠AOC的内部有一条射线OF,且∠AOC-4∠AOF=2∠BOE+∠AOF,试确定∠AOF与∠DOE的度数之间的关系,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店去年3至8月销售吐鲁番葡萄、哈密瓜的情况如下表:
3月
4月
5月
6月
7月
8月
吐鲁番葡萄(单位:百公斤)
4
8
5
8
10
13
哈密瓜(单位:百公斤)
8
7
9
7
10
7
(1)请你根据以上数据填写下表:
平均数/百公斤
方差
吐鲁番葡萄
8
9
哈密瓜
(2)请你根据上述信息,对这两种水果在去年3月份至8月份的销售情况进行分析.
相关试题

