【题目】某学校有两个校区:南校和北校,这两个校区九年级学生各有300名,为了解这两个校区九年级学生的英语单词掌握情况,进行了抽样调查,过程如下:
①收集数据,从南校和北校两个校区的九年级各随机抽取10名学生,进行英语单词测试,测试成绩(百分制)如下:
南校 92 100 86 89 73 98 54 95 98 85
北校 100 100 94 83 74 86 75 100 73 75
②整理、描述数据,按如下分数段整理、描述这两组样本数据:
成绩x 人数 部门 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
南校 | 1 | 0 | 1 | 3 | 5 |
北校 | 0 | 0 | 4 | 2 | 4 |
(说明:成绩90分及以上为优秀,80~89分分为良好,60~79分为合格,60分以下为不合格)
③分析数据,对上述数据进行分析,分别求出了两组样本数据的平均数、中位数、众数、方差如下表:
校区 | 平均数 | 中位数 | 众数 | 方差 |
南校 | 87 | 90.5 |
| 179.4 |
北校 | 86 |
|
| 121.6 |
④得出结论.
结合上述统计全过程,回答下列问题:
(1)补全③中的表格.
(2)请估计北校九年级学生英语单词掌握优秀的人数.
(3)你认为哪个校区的九年级学生英语单词掌握得比较好?说明你的理由.(至少从两个不同的角度说明推断的合理性)
参考答案:
【答案】(1)补全表格见解析;(2)估计北校九年级学生英语单词掌握优秀的人数为120人;(3)我认为南校区的九年级学生英语单词掌握得比较好,理由见解析.
【解析】
(1)一组数据中出现次数最多的数据叫做众数,依据已知条件即可补全③中的表格;
(2)依据![]() ×300,即可得到北校九年级学生英语单词掌握优秀的人数;(3)依据每个校区的英语测试的成绩的平均数以及中位线的高低,即可得到哪个校区的九年级学生英语单词掌握得比较好.
×300,即可得到北校九年级学生英语单词掌握优秀的人数;(3)依据每个校区的英语测试的成绩的平均数以及中位线的高低,即可得到哪个校区的九年级学生英语单词掌握得比较好.
(1)由题可得,南校区的九年级随机抽取的10名学生的成绩的众数为98,
北校区的九年级随机抽取的10名学生的成绩为:73、74、75、75、83、86、94、100、100、100,
∴北校区的九年级随机抽取的10名学生的成绩的中位数为:84.5;而众数为100;
故答案为:98,84.5,100;
(2)北校九年级学生英语单词掌握优秀的人数为:![]() ×300=120(人).
×300=120(人).
(3)我认为南校区的九年级学生英语单词掌握得比较好,理由如下:
①南校区的九年级学生在英语单词测试中,平均数较高,表示南校区的九年级学生的英语单词掌握情况较好;
②南校区的九年级学生在英语单词测试中,中位数较高,表示南校区英语单词掌握优秀的学生较多.(答案不唯一)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△CAD与△CEB都是等边三角形,BD、EA的延长线相交于点F.
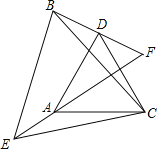
(1)求证:△ACE≌△DCB.
(2)求∠F的度数.
(3)若AD⊥BD,请直接写出线段EF与线段BD、DF之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣ x2+bx+c经过点A,B.
x2+bx+c经过点A,B.(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

-
科目: 来源: 题型:
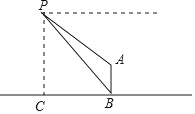
查看答案和解析>>【题目】如图,一个热气球悬停在空中,从热气球上的P点测得直立于地面的旗杆AB的顶端A与底端B的俯角分别为34°和45°,此时P点距地面高度PC为75米,求旗杆AB的高度(结果精确到0.1米).
(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67)
-
科目: 来源: 题型:
查看答案和解析>>【题目】超市老板大宝第一次用1000元购进某种商品,由于畅销,这批商品很快售完,第二次去进货时发现批发价上涨了5元,购买与第一次相同数量的这种商品需要1250元.
(1)求第一次购买这种商品的进货价是多少元?
(2)若这两批商品的售价均为32元,问这两次购进的商品全部售完(不考虑其它因素)能赚多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O在△ABC内,且知OB和OC分别平分∠ABC和∠ACB,过O作直线EF分别交AB、AC于E、F.
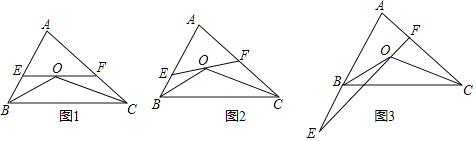
(1)如图1,已知EF∥BC.
①若∠A=76°,请直接写出∠BOE+∠COF的度数;
②猜想∠BOE、∠COF与∠A之间有怎样的数量关系?写出结论,不用证明
(2)直线EF绕点O旋转到如图2的位置时(EF与BC不平行),那么上面(1)②中猜想的结论还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
(3)当直线EF绕点O旋转到如图3的位置时(点E在AB的延长线上),请直接写出∠BOE、∠COF与∠A之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
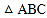 中,
中,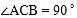 ,D是AB上的点,过点D作
,D是AB上的点,过点D作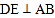 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,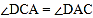 ,则下列结论正确的有( )
,则下列结论正确的有( )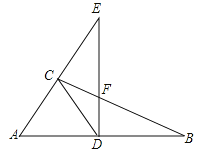
①∠DCB=∠B;②CD=
 AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.A. ①②③ B. ①②④ C. ②③④ D. ①②③④
相关试题

