【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
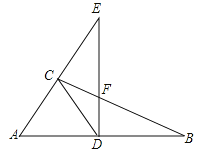
①∠DCB=∠B;②CD=![]() AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
参考答案:
【答案】B
【解析】
由在△ABC中,∠ACB=90°,DE⊥AB,根据等角的余角相等,可得①∠DCB=∠B正确;
由①可证得AD=BD=CD,即可得②CD=![]() AB正确;
AB正确;
易得③△ADC是等腰三角形,但不能证得△ADC是等边三角形;
由若∠E=30°,易求得∠FDC=∠FCD=30°,则可证得DF=CF,继而证得DE=EF+CF.
在△ABC中,∵∠ACB=90°,DE⊥AB,∴∠ADE=∠ACB=90°,∴∠A+∠B=90°,∠ACD+∠DCB=90°.
∵∠DCA=∠DAC,∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD.
∵AD=BD,∴CD=![]() AB;故②正确;
AB;故②正确;
∠DCA=∠DAC,∴AD=CD,但不能判定△ADC是等边三角形;故③错误;
∵∠E=30°,∴∠A=60°,∴△ACD是等边三角形,∴∠ADC=30°.
∵∠ADE=∠ACB=90°,∴∠EDC=∠BCD=∠B=30°,∴CF=DF,∴DE=EF+DF=EF+CF.故④正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的菱形ABCD中,∠A=60°,M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,则线段A′C长度的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
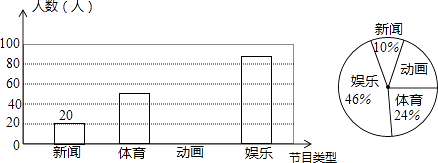
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解2017年八年级学生课外书籍借阅情况.从中随机抽取了40名学生进行调查,根据调查结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类本数占这40名学生借阅总本数的40%.

(1)求表格中字母m的值及扇形统计图中“教辅类”所对应的圆心角α的度数;
(2)该校2017年八年级有500名学生,请你估计该年级学生共借阅教辅类书籍约多少本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.

(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想. -
科目: 来源: 题型:
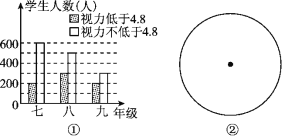
查看答案和解析>>【题目】某学习小组对所在城区初中学生的视力情况进行抽样调查,图①是调查小组根据调查结果画出的条形统计图.请根据图中信息解决下列问题:
(1)本次调查活动中共抽查了多少名学生?
(2)请估算该城区视力不低于4.8的学生所占的比例,用扇形统计图的形式在图②中表示出来.
(3)假设该城区八年级共有4 000名学生,请估计这些学生中视力低于4.8的学生约有多少名.
相关试题

