【题目】如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心, ![]() AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC. 
(1)求证:D是 ![]() 的中点;
的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若 ![]() ,且AC=4,求CF的长.
,且AC=4,求CF的长.
参考答案:
【答案】
(1)证明:∵AC是⊙O的直径,
∴∠AEC=90°,
∴AE⊥BC,
∵OD∥BC,
∴AE⊥OD,
∴D是 ![]() 的中点;
的中点;
(2)证明:
方法一:
如图,延长OD交AB于G,则OG∥BC,

∴∠AGD=∠B,
∵∠ADO=∠BAD+∠AGD,
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠DAO=∠B+∠BAD;
方法二:
如图,延长AD交BC于H,
则∠ADO=∠AHC,
∵∠AHC=∠B+∠BAD,
∴∠ADO=∠B+∠BAD,
又∵OA=OD,
∴∠DAO=∠B+∠BAD;
(3)解:∵AO=OC,
∴S△OCD= ![]() S△ACD,
S△ACD,
∵ ![]() ,
,
∴ ![]() ,
,
∵∠ACD=∠FCE,∠ADC=∠FEC=90°,
∴△ACD∽△FCE,
∴ ![]() ,
,
即: ![]() ,
,
∴CF=2.
【解析】(1)由AC是⊙O的直径,即可求得OD∥BC,又由AE⊥OD,即可证得D是 ![]() 的中点;(2)首先延长OD交AB于G,则OG∥BC,可得OA=OD,根据等腰三角形的性质,即可求得∠DAO=∠B+∠BAD;(3)由AO=OC,S△OCD=
的中点;(2)首先延长OD交AB于G,则OG∥BC,可得OA=OD,根据等腰三角形的性质,即可求得∠DAO=∠B+∠BAD;(3)由AO=OC,S△OCD= ![]() S△ACD , 即可得
S△ACD , 即可得 ![]() ,又由△ACD∽△FCE,根据相似三角形的面积比等于相似比的平方,即可求得CF的长.
,又由△ACD∽△FCE,根据相似三角形的面积比等于相似比的平方,即可求得CF的长.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求证:角平分线上的点到这个角的两边距离相等. 已知:
求证:
证明: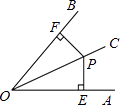
-
科目: 来源: 题型:
查看答案和解析>>【题目】“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用“五一”假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:
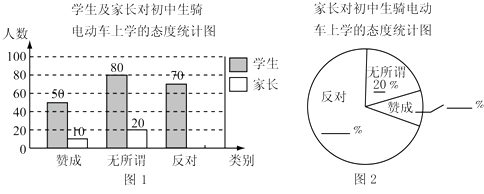
(1)这次抽查的家长总人数为为多少;
(2)请补全条形统计图和扇形统计图;
(3)从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒.
(1)设敬老院有x名老人,则这批牛奶共有多少盒?(用含x的代数式表示).
(2)该敬老院至少有多少名老人?最多有多少名老人? -
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
请结合图表完成下列各题:

(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图.
的图象如图.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )

A. ﹣
﹣ 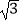
B. ﹣2
﹣2 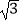
C.π﹣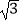
D. ﹣
﹣ 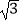
相关试题

