【题目】已知二次函数 ![]() 的图象如图.
的图象如图.
(1)求它的对称轴与x轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
参考答案:
【答案】
(1)
解:由 ![]() ,
,
得x=﹣ ![]() =﹣
=﹣  =3,
=3,
∴D(3,0);
(2)
解:方法一:
如图1,

设平移后的抛物线的解析式为 ![]() ,
,
则C(0,k)OC=k,
令y=0即 ![]() ,
,
得 ![]() ,
, ![]() ,
,
∴A ![]() ,B
,B ![]() ,
,
∴ ![]() ,
,
![]() =2k2+8k+36,
=2k2+8k+36,
∵AC2+BC2=AB2
即:2k2+8k+36=16k+36,
得k1=4,k2=0(舍去),
∴抛物线的解析式为 ![]() ,
,
方法二:
∵ ![]() ,∴顶点坐标
,∴顶点坐标 ![]() ,
,
设抛物线向上平移h个单位,则得到C(0,h),顶点坐标 ![]() ,
,
∴平移后的抛物线: ![]() ,
,
当y=0时, ![]() ,得
,得 ![]() ,
, ![]() ,
,
∴A ![]() ,B
,B ![]() ,
,
∵∠ACB=90°,
∴△AOC∽△COB,则OC2=OAOB,
即 ![]() ,
,
解得h1=4,h2=0(不合题意舍去),
∴平移后的抛物线: ![]() ;
;
(3)
解:方法一:
如图2,

由抛物线的解析式 ![]() 可得,
可得,
A(﹣2,0),B(8,0),C(0,4),M ![]() ,
,
过C、M作直线,连接CD,过M作MH垂直y轴于H,则MH=3,
∴ ![]() ,
,
![]() ,
,
在Rt△COD中,CD= ![]() =AD,
=AD,
∴点C在⊙D上,
∵ ![]()
![]() ,
,
∴DM2=CM2+CD2
∴△CDM是直角三角形,∴CD⊥CM,
∴直线CM与⊙D相切.
方法二:
如图3,

由抛物线的解析式可得A(﹣2,0),B(8,0),C(0,4),M ![]() ,
,
作直线CM,过D作DE⊥CM于E,过M作MH垂直y轴于H,则MH=3, ![]() ,由勾股定理得
,由勾股定理得 ![]() ,
,
∵DM∥OC,
∴∠MCH=∠EMD,
∴Rt△CMH∽Rt△DME,
∴ ![]() 得DE=5,
得DE=5,
由(2)知AB=10,∴⊙D的半径为5.
∴直线CM与⊙D相切.
【解析】(1)根据对称轴公式求出x=﹣ ![]() ,求出即可;(2)假设出平移后的解析式即可得出图象与x轴的交点坐标,再利用勾股定理求出即可;(3)由抛物线的解析式
,求出即可;(2)假设出平移后的解析式即可得出图象与x轴的交点坐标,再利用勾股定理求出即可;(3)由抛物线的解析式 ![]() 可得,A,B,C,M各点的坐标,再利用勾股定理逆定理求出CD⊥CM,即可证明.
可得,A,B,C,M各点的坐标,再利用勾股定理逆定理求出CD⊥CM,即可证明.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院慰问孤寡老人,如果给每个老人分5盒,则剩下38盒,如果给每个老人分6盒,则最后一个老人不足5盒,但至少分得一盒.
(1)设敬老院有x名老人,则这批牛奶共有多少盒?(用含x的代数式表示).
(2)该敬老院至少有多少名老人?最多有多少名老人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,
 AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC. 
(1)求证:D是 的中点;
的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若 ,且AC=4,求CF的长.
,且AC=4,求CF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
请结合图表完成下列各题:

(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )

A. ﹣
﹣ 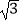
B. ﹣2
﹣2 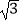
C.π﹣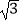
D. ﹣
﹣ 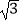
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象,下列结论: ①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为﹣1;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为 .

相关试题

