搜索
【题目】如图，正方形ABCD的两边BC，AB分别在平面直角坐标系的x轴、y轴的正半轴上，正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形，已知AC=3 
，若点A′的坐标为（1，2），则正方形A′B′C′D′与正方形ABCD的相似比是（ ）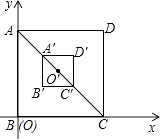 
A.
B.
C.
D.
参考答案：
【答案】B
【解析】解：∵在正方形ABCD中，AC=3 
∴BC=AB=3，
延长A′B′交BC于点E，
∵点A′的坐标为（1，2），
∴OE=1，EC=A′E=3﹣1=2，
∴OE：BC=1：3，
∴AA′：AC=1：3，
∵AA′=CC′，
∴AA′=CC′=A′C′，
∴A′C′：AC=1：3，
∴正方形A′B′C′D′与正方形ABCD的相似比是 
．
故选B．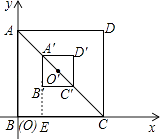
【考点精析】掌握位似变换是解答本题的根本，需要知道它们具有相似图形的性质外还有图形的位置关系（每组对应点所在的直线都经过同一个点—位似中心）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长方形ABCD中，AB：BC=3：4，AC=5，点P从点A出发，以每秒1个单位的速度，沿△ABC边A→B→C→A的方向运动，运动时间为t秒．
（1）求AB与BC的长；
（2）在点P的运动过程中，是否存在这样的点P，使△CDP为等腰三角形？若存在，求出t值；若不存在，说明理由．
-
科目： 来源： 题型：
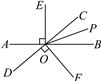
查看答案和解析>>【题目】如图，直线AB与CD相交于点O，OP是∠BOC的平分线，EO⊥AB于点O，FO⊥CD于点O.
(1)图中除直角外，还有其他相等的角，请写出两对：①______________；②______________．
(2)如果∠AOD＝40°，那么：
①根据__________，可得∠BOC＝________；
②求∠POF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠1＝∠2，DE⊥BC，AB⊥BC，试说明：∠A＝∠3.
解：因为DE⊥BC，AB⊥BC(已知)，
所以∠DEC＝∠ABC＝90°(____________)，
所以DE∥AB(____________________)，
所以∠2＝________(____________________)，
∠1＝________(____________________)．
因为∠1＝∠2(已知)，
所以∠A＝∠3(等量代换)．
-
科目： 来源： 题型：
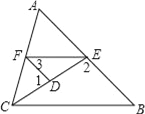
查看答案和解析>>【题目】如图，已知∠1，∠2互为补角，且∠3=∠B，
(1)求证：∠AFE=∠ACB
(2)若CE平分∠ACB，且∠1=80°，∠3=45°，求∠AFE的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为直线x=1，有如下结论：
①c＜1；
②2a+b=0；
③b2＜4ac；
④若方程ax2+bx+c=0的两根为x1 ， x2 ， 则x1+x2=2．
则正确的结论是（ ）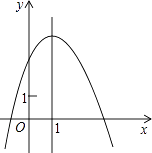
A.①②
B.①③
C.②④
D.③④ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在△ABC中，D是BA延长线上一点，AE是∠DAC的平分线，P是AE上的一点（点P不与点A重合），连接PB，PC．通过观察，测量，猜想PB+PC与AB+AC之间的大小关系，并加以证明．
相关试题
