【题目】已知:如图,在△ABC中,D是BA延长线上一点,AE是∠DAC的平分线,P是AE上的一点(点P不与点A重合),连接PB,PC.通过观察,测量,猜想PB+PC与AB+AC之间的大小关系,并加以证明.

参考答案:
【答案】PB+PC>AB+AC.
【解析】
根据全等三角形的判定与性质,可得FP=CP,根据三角形的两边之和大于第三边,可得答案.
PB+PC>AB+AC.
证明如下:如图,在BA的延长线上截取AF=AC,连接PF.
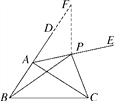
∵AE平分∠DAC,
∴∠FAP=∠CAP.
在△FAP和△CAP中,
AF=AC,∠FAP=∠CAP,AP=AP,
∴△FAP≌△CAP(SAS),
∴FP=CP.
在△FPB中,FP+BP>FA+AB,
即PB+PC>AB+AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】88层的金茂大厦的电梯上,有显示楼层的液晶屏,如图,可显示01,02,…,88,由于屏幕受到损坏,显示左边数字的7根线段中有1根不能亮了,显示右边数字的7根线段中有3根不能亮了。请问:电梯在运行的过程中,最多还有 _____个楼层的数字显示是正确的.

(说明)数字0、1、2、3、4、5、6、7、8、9显示方式如下图所示.


-
科目: 来源: 题型:
查看答案和解析>>【题目】一张长方形纸片,剪下一个正方形,剩下一个长方形,称为第一次操作;在剩下的长方形纸片中再剪下一个正方形,剩下一个长方形,称为第二次操作;…;若在第n次操作后,剩下的长方形为正方形,则称原长方形为n阶奇异长方形.如图1,长方形ABCD中,若AB=2,BC=6,则称长方形ABCD为2阶奇异长方形.

(1)判断与操作:如图2,长方形ABCD长为10,宽为6,它是奇异长方形,请写出它是____阶奇异长方
形,并在图中画出裁剪线;
探究与计算:已知长方形ABCD的一边长为24,另一边长为a (a<24),且它是3阶奇异长方形,请画出所
有可能的长方形ABCD及裁剪线的示意图,并求出相应的a值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;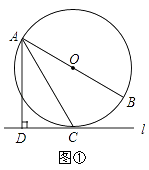
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF.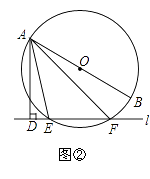
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题一:如图1,已知A,C两点之间的距离为16 cm,甲,乙两点分别从相距3cm的A,B两点同时出发到C点,若甲的速度为8 cm/s,乙的速度为6 cm/s,设乙运动时间为x(s), 甲乙两点之间距离为y(cm).
(1)当甲追上乙时,x = .
(2)请用含x的代数式表示y.
当甲追上乙前,y= ;
当甲追上乙后,甲到达C之前,y= ;
当甲到达C之后,乙到达C之前,y= .

问题二:如图2,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(1)分针OD指向圆周上的点的速度为每分钟转动 cm;时针OE指向圆周上的点的速度为每分钟转动 cm.
(2)若从4:00起计时,求几分钟后分针与时针第一次重合.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三条角平分线相交于点I,过点I作DI⊥IC,交AC于点D.
(1)如图①,求证:∠AIB=∠ADI;
(2)如图②,延长BI,交外角∠ACE的平分线于点F.
①判断DI与CF的位置关系,并说明理由;
②若∠BAC=70°,求∠F的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
相关试题

