【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
参考答案:
【答案】(1)证明见解析;
(2)∠EOC的度数是40°;
(3)不改变,∠OCB:∠OFB的值为1:2.
【解析】分析:(1),首先根据平行线的性质可得∠B+∠O=180°,再根据∠A=∠B可得∠A+∠O=180°,进而得到OB∥AC;
(2)由(1)即可求出∠BOA的度数,根据角平分线的性质可得∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,进而得到∠EOC的大小;
∠FOA,进而得到∠EOC的大小;
(3)由BC∥OA可得∠FCO=∠COA,进而得到∠FOC=∠FCO,故∠OFB=∠FOC+∠FCO=2∠OCB,进而得到∠OCB:∠OFB的值.
本题解析;(1)证明:∵BC∥OA,
∴∠B+∠O=180°,∴∠O=180°﹣∠B=80°,
而∠A=100°,∴∠A+∠O=180°,
∴OB∥AC;
(2)解:∵OE平分∠BOF,
∴∠BOE=∠FOE, 而∠FOC=∠AOC,
∴∠EOF+∠COF=![]() ∠AOB=
∠AOB=![]() ×80°=40°;
×80°=40°;
(3)解:不改变
∵BC∥OA,
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠FOC=∠AOC,
∴∠AOF=2∠AOC,
∴∠OFB=2∠OCB,即∠OCB:∠OFB的值为1:2;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中真命题是( )
A. 同旁内角相等,两直线平行
B. 两锐角之和为钝角
C. 到角的两边距离相等的点在这个角的平分线上
D. 直角三角形斜边上的中线等于斜边的一半
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形具有而平行四边形不一定具有的性质是( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
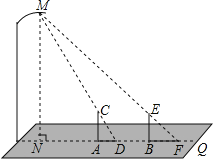
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,AB为⊙O的直径,AC是弦,
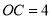 ,
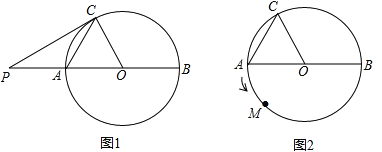
,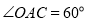 .
.
(1)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(2)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动一周,当
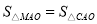 时,求半径OM所扫过的扇形的面积.
时,求半径OM所扫过的扇形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了考察一批电视机的使用寿命,从中任意抽取了10台进行实验,在这个问题中样本是( )
A.抽取的10台电视机
B.这一批电视机的使用寿命
C.10
D.抽取的10台电视机的使用寿命 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=a(x﹣2)2+c(a>0),当自变量x分别取1.5、3、0时,对应的函数值分别为y1 , y2 , y3 , 则y1 , y2 , y3的大小关系是 .
相关试题

