【题目】在⊙O中,AB为⊙O的直径,AC是弦,![]() ,
,![]() .
.
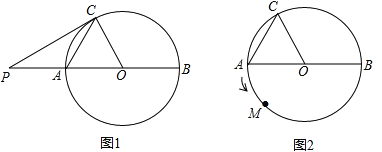
(1)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(2)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动一周,当![]() 时,求半径OM所扫过的扇形的面积.
时,求半径OM所扫过的扇形的面积.
参考答案:
【答案】(1)8;(2)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
试题分析:(1)根据切线的性质得到CP⊥OC,由于∠OAC=∠AOC=60°,于是得到∠P=90°-∠AOC=30°,在Rt△POC中,求得CO=![]() PO=4,即可得到结论;
PO=4,即可得到结论;
(2)如图,当S△MAO=S△CAO时,动点M的位置有四种.①作点C关于直径AB的对称点M1,连接AM1,OM1,②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得弧AM的长,即可得到结论.
试题解析:(1)∵CP与⊙O相切,OC是半径.
∴CP⊥OC,
又∵∠OAC=∠AOC=60°,
∴∠P=90°-∠AOC=30°,
∴在Rt△POC中,CO=![]() PO=4,
PO=4,
则PO=2CO=8;
(2)如图,

①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得S△M1AO=S△CAO,∠AOM1=60°∴当点M运动到M1时,S△MAO=S△CAO,
此时点M经过的弧长为![]() ,
,
∴半径OM所扫过的扇形的面积=![]() ;
;
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO.
∴∠AOM1=∠M1OM2=∠BOM2=60°
∴![]() 或
或![]() ,
,
∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为![]() ,
,
∴半径OM所扫过的扇形的面积=![]() ×
×![]() ×4=
×4=![]() π;
π;
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO=S△CAO
∴∠BOM3=60°,
∴![]() =
=![]() ×240或
×240或![]() =
=![]() ×2=
×2=![]()
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为![]() ,
,
∴半径OM所扫过的扇形的面积=![]() ×
×![]() ×4=
×4=![]() ;
;
④当点M运动到C时,M与C重合,S△MAO=S△CAO,
此时点M经过的弧长为![]() ×300°或
×300°或![]() π+
π+![]() =
=![]()
∴半径OM所扫过的扇形的面积=![]() ×
×![]() ×4=
×4=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形具有而平行四边形不一定具有的性质是( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】晚饭后,小林和小京在社区广场散步,两人在灯下沿直线NQ移动,如图,当小林正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小京正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小林的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小京身高BE的长.(结果精确到0.01米)
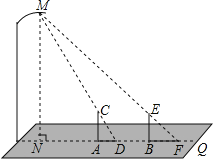
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了考察一批电视机的使用寿命,从中任意抽取了10台进行实验,在这个问题中样本是( )
A.抽取的10台电视机
B.这一批电视机的使用寿命
C.10
D.抽取的10台电视机的使用寿命 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=a(x﹣2)2+c(a>0),当自变量x分别取1.5、3、0时,对应的函数值分别为y1 , y2 , y3 , 则y1 , y2 , y3的大小关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】深圳今年4月份某星期的最高气温如下(单位℃):26,25,27,28,27,25,25,则这个星期的最高气温的众数和中位数分别是( )
A.25,26 B.25,26.5 C.27,26 D.25,28
相关试题

