【题目】根据提示填空(8分)
如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.

因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
参考答案:
【答案】见解析.
【解析】分析:根据平行线的性质推出∠1=∠2=∠3,推出AB∥DG,根据平行线的性质得出![]() 代入求出即可.
代入求出即可.
详解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
∵![]()
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线l经过A、C两点.
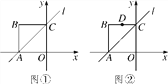
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;
(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.
①请求出|BE+DE|的最小值和此时点E的坐标;
②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|的最大值,并写出此时点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在方格纸中,
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)把△ABC向右平移6个单位长度,再向上平移2个单位长度,画出平移后的图 形△A′B′C′;
(3)计算△A′B′C′的面积S .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的横坐标表示两车第二次相遇的时间;⑤点E的坐标为(7,180)其中正确的有________(把所有正确结论的序号都填在横线上).
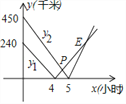
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x﹣3的正比例函数,且当x=2时,y=﹣3.
(1)求y与x之间的函数关系式;
(2)求当x=1时,y的值;
(3)求当y=﹣12时,x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8,AD=BC=6,D点与原点重合,坐标为(0,0).
(1)直接写出点B的坐标__________.
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥y轴?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.

(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
相关试题

