【题目】如图,△ABC在方格纸中,
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)把△ABC向右平移6个单位长度,再向上平移2个单位长度,画出平移后的图 形△A′B′C′;
(3)计算△A′B′C′的面积S .

参考答案:
【答案】(1)(2,1);(2)![]() ,
, ![]() ,
, ![]() ;(3)4
;(3)4
【解析】分析:(1)由点A(2,3)向左平移2个单位,向下平移3个单位的点为坐标原点,水平方向为x轴,竖直方向为y轴建立平面直角坐标系,然后写出点B的坐标即可;
(2)根据平移的方向:向右平移6个单位,再向上平移2个单位,在网格结构中找出点![]() 平移后的对应点
平移后的对应点![]() 的位置,然后顺次连接即可;
的位置,然后顺次连接即可;
(3)根据网格得到![]() 以及
以及![]() 边上的高的长,再根据三角形的面积公式即可完成解答.
边上的高的长,再根据三角形的面积公式即可完成解答.
详解:(1)建立平面直角坐标系如图所示,则点B的坐标为![]()
(2)![]() 如图所示:
如图所示:

(3)观察图形可知![]() =2,边
=2,边![]() 上的高为4,
上的高为4,
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】这个周末,七年级准备组织观看电影《我和我的祖国》,由各班班长负责买票,一班班长问售票员买团体票是否可以优惠,售票员说:50人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;
方案二:若打9折,有6人可以免票.
一班班长思考了一会儿,说我们班无论选择哪种方案要付的钱是一样的,请问一班有几人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程4x=8变形为x=2,其依据是( )
A.等式的性质1B.等式的性质2C.分式的基本性质D.不等式的性质1
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线l经过A、C两点.
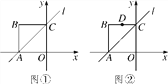
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;
(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.
①请求出|BE+DE|的最小值和此时点E的坐标;
②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|的最大值,并写出此时点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的高速公路上依次有3个标志点A、B、C,甲、乙两车分别从A、C两点同时出发,匀速行驶,甲车从A→B→C,乙车从C→B→A,甲、乙两车离B的距离y1、y2(千米)与行驶时间x(小时)之间的函数关系图象如图所示.观察图象,给出下列结论:①A、C之间的路程为690千米;②乙车比甲车每小时快30千米;③4.5小时两车相遇;④点E的横坐标表示两车第二次相遇的时间;⑤点E的坐标为(7,180)其中正确的有________(把所有正确结论的序号都填在横线上).
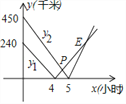
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据提示填空(8分)
如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.

因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x﹣3的正比例函数,且当x=2时,y=﹣3.
(1)求y与x之间的函数关系式;
(2)求当x=1时,y的值;
(3)求当y=﹣12时,x的值.
相关试题

