【题目】如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 
(1)求证:AC是⊙O的切线;
(2)求弦BD的长;
(3)求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OC,OC交BD于E,

∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∵∠CDB=∠OBD,
∴CD∥AB,
又∵AC∥BD,
∴四边形ABDC为平行四边形,
∴∠A=∠D=30°,
∴∠OCA=180°﹣∠A﹣∠COB=90°,即OC⊥AC
又∵OC是⊙O的半径,
∴AC是⊙O的切线
(2)解:由(1)知,OC⊥AC.
∵AC∥BD,
∴OC⊥BD,
∴BE=DE,
∵在直角△BEO中,∠OBD=30°,OB=6,
∴BE=OBcos30°=3 ![]() ,
,
∴BD=2BE=6 ![]()
(3)解:易证△OEB≌△CED,
∴S阴影=S扇形BOC
∴S阴影= ![]() =6π.
=6π.
答:阴影部分的面积是6π
【解析】(1)连接OC,OC交BD于E,由∠CDB=∠OBD可知,CD∥AB,又AC∥BD,四边形ABDC为平行四边形,则∠A=∠D=30°,由圆周角定理可知∠COB=2∠D=60°,由内角和定理可求∠OCA=90°,证明切线;(2)利用(1)中的切线的性质和垂径定理以及解直角三角形来求BD的长度;(3)证明△OEB≌△CED,将阴影部分面积问题转化为求扇形OBC的面积.
【考点精析】解答此题的关键在于理解垂径定理的推论的相关知识,掌握推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据提示填空(8分)
如图,EF∥AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.

因为EF∥AD
所以∠2=____(____________________________)
又因为∠1=∠2
所以∠1=∠3(______________)
所以AB∥_____(_____________________________)
所以∠BAC+______=180°(_____________________)
因为∠BAC=80° 所以∠AGD=_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x﹣3的正比例函数,且当x=2时,y=﹣3.
(1)求y与x之间的函数关系式;
(2)求当x=1时,y的值;
(3)求当y=﹣12时,x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8,AD=BC=6,D点与原点重合,坐标为(0,0).
(1)直接写出点B的坐标__________.
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t秒,当t为何值时,PQ∥y轴?

-
科目: 来源: 题型:
查看答案和解析>>【题目】从正面看一个底面直径为10cm的圆柱体饮料杯子如图所示,在它的正中间竖直插入一根吸管(吸管在杯口一端的位置固定不动),吸管露出杯子外1cm,当吸管伸向杯壁底部时,吸管顶端刚好与杯口高度平齐.
(1)求杯子的高度;
(2)若吸管伸出杯口的长度至少为0.5cm时,才方便喝饮料,则吸管至少应设计为多长?
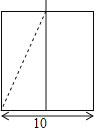
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣
 x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:DE=DF;
(2)若∠A=
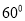 ,BE=5.
,BE=5.①求证:
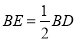 ②求△ABC的周长.
②求△ABC的周长. 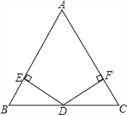
相关试题

