【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
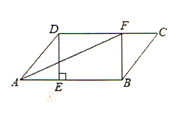
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
参考答案:
【答案】(1)详见解析;(2)20.
【解析】试题分析:(1)根据有一个角是90度的平行四边形是矩形可判定,
(2)首先证明AD=DF,求出AD即可解决问题.
试题解析: (1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,即BE∥DF,
∵CF=AE,
∴DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形.
(2)因为AB∥CD ,所以∠BAF=∠AFD,因为AF平分∠BAD,所以∠DAF=∠AFD,所以AD=DF,在直角三角形ADE中,因为AE=3,DE=4,所以AD=5,所以矩形的面积为20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
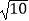 ,BC边上的高AD=6,则另一边BC等于( )
,BC边上的高AD=6,则另一边BC等于( )
A.10
B.8
C.6或10
D.8或10 -
科目: 来源: 题型:
查看答案和解析>>【题目】小张的爸爸在上周星期六骑摩托车带小张和弟弟到离家27千米的游乐园玩耍,爸爸自己骑摩托车的速度为26千米
 时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米
时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米 时,当天三人同时从家出发,弟弟以4千米
时,当天三人同时从家出发,弟弟以4千米 时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、
时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、 爸爸骑摩托车掉头和停放摩托车的时间忽略不计
爸爸骑摩托车掉头和停放摩托车的时间忽略不计 问:小张搭乘摩托车的路程为______千米.
问:小张搭乘摩托车的路程为______千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°.
(1)若a:b=3:4,c=10,则a=_______,b=_______;
(2)若a=6,b=8,则斜边c上的高h=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏,A型日光灯每盏进价为40元,售价为60元,B型日光灯每盏进价为50元,售价为80元.
(1)求10月份两种新型节能日光灯各购进多少盏?
(2)将10月份购买的日光灯从生产基地运往商场的过程中,A型日光灯出现
 的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润
的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润 型日光灯在原售价基础上提高
型日光灯在原售价基础上提高 ,问A型日光灯调整后的售价为多少元?
,问A型日光灯调整后的售价为多少元?(3)进入11月份,B型日光灯的需求量增大,于是商场在筹备“双十一”促销活动时,决定去甲、乙两个生产基地只购进一批B型日光灯,甲、乙生产基地给出了不同的优惠措施:
甲生产基地:B型日光灯出厂价为每盏50元,折扣如表一所示
乙生产基地:B型日光灯出厂价为每盏47元,同时当出厂总金额达一定数量后还可按表二返现金.
表一
甲生产基地
一次性购买的数量
折扣数
不超过150盏的部分
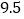 折
折超过150盏的部分
9折
表二
乙生产基地
出厂总金额
返现金
不超过5640元
0元
超过5640元,但不超过9353元
返现300元
超过9353元
先返现出厂总金额的
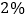 后,再返现206元
后,再返现206元已知该商场在甲生产基地购买B型日光灯共支付7350元,在乙生产基地购买B型日光灯共支付9006元,若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
相关试题

