【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
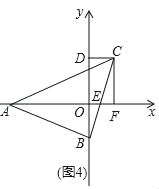
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).

参考答案:
【答案】(1)C(﹣1,4);(2)OD=a﹣b;(3)aAE+bCF=﹣a(a+b).
【解析】
(1)先确定出OA=3,OB=1,进而判断出△AOB≌△BDC,即可得出BD=3,CD=1,即可得出结论;
(2)分三种情况,同(1)的方法即可得出结论;
(3)先确定出OF=CD=﹣b,CF=OD=b﹣a,进而得出AF=OA+OF=﹣a﹣b,在判断出△AOB∽△CFE,即可得出EF=![]() (b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣
(b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),即可得出结论.
(b﹣a),即可得出结论.
解:(1)如图1,
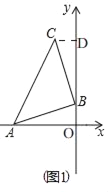
∵点A的坐标为(﹣3,0),点B的坐标为(0,1),
∴OA=3,OB=1,
过点C作CD⊥y轴于D,
∴∠BCD+∠CBD=90°,
∵∠ABC=90°,
∴∠CBD+∠ABO=90°,
∴∠ABO=∠BCD,
在△AOB和△BDC中,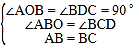 ,
,
∴△AOB≌△BDC,
∴BD=OA=3,CD=OB=1,
∴OD=OB+BD=4,
∴C(﹣1,4);
(2)当点B在y轴正半轴上时,
如图1,∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=b,
∴OD=OB+BD=b+(﹣a)=b﹣a,
当点B在y轴负半轴上,点C在第一象限时,如图2,
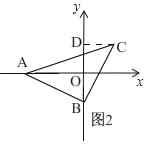
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
当点B在y轴负半轴,点C在第四象限时,如图3,
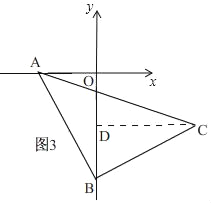
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=OB﹣BD=﹣b﹣(﹣a)=a﹣b;
(3)如图4,
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
∵CF⊥OA于F,
∴四边形ODCF是矩形,
∴OF=CD=﹣b,CF=OD=b﹣a,
∴AF=OA+OF=﹣a﹣b,
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵AF平分∠BAC,
∴∠OAC=∠OAB=22.5°,
∴∠ECF=∠ACF﹣∠ACB=90°﹣∠OAC﹣∠ACB=22.5°=∠OAB,
∵∠AOB=∠CFE,
∴△AOB∽△CFE,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() (b﹣a),
(b﹣a),
∴AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),
(b﹣a),
∵CF=b﹣a,
∴AE=﹣a﹣b﹣![]() CF,
CF,
∴aAE+bCF=﹣a(a+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
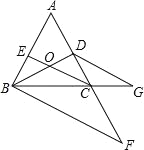
A. 6个 B. 5个 C. 4个 D. 3个
-
科目: 来源: 题型:
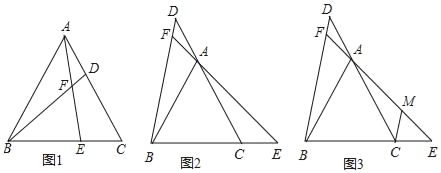
查看答案和解析>>【题目】已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
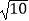 ,BC边上的高AD=6,则另一边BC等于( )
,BC边上的高AD=6,则另一边BC等于( )
A.10
B.8
C.6或10
D.8或10 -
科目: 来源: 题型:
查看答案和解析>>【题目】小张的爸爸在上周星期六骑摩托车带小张和弟弟到离家27千米的游乐园玩耍,爸爸自己骑摩托车的速度为26千米
 时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米
时,由于摩托车后座只能搭乘一人,搭一人的速度为24千米 时,当天三人同时从家出发,弟弟以4千米
时,当天三人同时从家出发,弟弟以4千米 时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、
时的速度步行,爸爸带小张骑摩托车行驶一定路程后,小张下车以6千米时的速度步行前往游乐园,爸爸返回接弟弟,接上弟弟后直接去游乐园排队买票,爸爸花了5分钟买好票,此时小张也正好到达、 爸爸骑摩托车掉头和停放摩托车的时间忽略不计
爸爸骑摩托车掉头和停放摩托车的时间忽略不计 问:小张搭乘摩托车的路程为______千米.
问:小张搭乘摩托车的路程为______千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
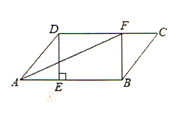
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
相关试题

