【题目】如图,相距2cm的两个点A、B在直线l上.它们分别以2cm/s和1cm/s的速度在l上同时向右平移,当点A,B分别平移到点A1 , B1的位置时,半径为1cm的⊙A1 , 与半径为BB1的⊙B相切.则点A平移到点A1 , 所用的时间为s. ![]()
参考答案:
【答案】![]() 或3
或3
【解析】解:设点A平移到点A1 , 所用的时间为ts, 根据题意得:AB=2cm,AA1=2tcm,A1B=(2﹣2t)cm,BB1=tcm,
如图,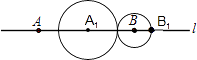
此时外切:2﹣2t=1+t,
∴t= ![]() ;
;
如图,此时内切:2﹣2t=1﹣t,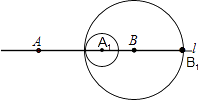
∴t=1,此时两圆心重合,舍去;
或2﹣2t=t﹣1,
解得:t=1,此时两圆心重合,舍去;
如图,此时内切:2t﹣t+1=2,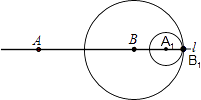
∴t=1,此时两圆心重合,舍去;
如图:此时外切:2t﹣t﹣1=2,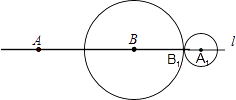
∴t=3.
∴点A平移到点A1 , 所用的时间为1(此时两圆重合,舍去)或3s.
所以答案是: ![]() 或3.
或3.
【考点精析】通过灵活运用圆与圆的位置关系,掌握两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师从“淋浴龙头”受到启发.编了一个题目: 在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当m=
 时,求n的值.
时,求n的值.
你解答这个题目得到的n值为( )
A.4﹣2
B.2 ﹣4
﹣4
C.
D.
-
科目: 来源: 题型:
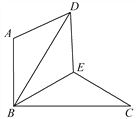
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】取一张矩形纸片按照图1、图2中的方法对折,并沿图3中过矩形顶点的斜线(虚线)剪开,把剪下的①这部分展开,平铺在桌面上.若平铺的这个图形是正六边形,则这张矩形纸片的宽和长之比为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A
 B
B C
C ;
;(2) 请画出△ABC关于原点对称的△A
 B
B C
C ;
;(3) 在
 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下面各题
(1)计算: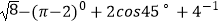
(2)先化简.再求值:a(a﹣2b)+2(a+b)(a﹣b)+(a+b)2 , 其中a=﹣ ,b=1.
,b=1. -
科目: 来源: 题型:
查看答案和解析>>【题目】为调查学生的身体素质,随机抽取了某市的若干所初中学校,根据学校学生的肺活量指标等级绘制了相应的统计图,如图. 根据以上统计图,解答下列问题:
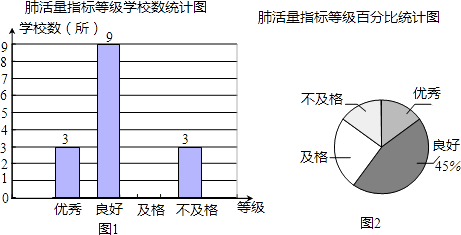
(1)这次调查共抽取了几所学校?请补全图1;
(2)估计该市140所初中学校中,有几所学校的肺活量指标等级为优秀?
相关试题

