【题目】取一张矩形纸片按照图1、图2中的方法对折,并沿图3中过矩形顶点的斜线(虚线)剪开,把剪下的①这部分展开,平铺在桌面上.若平铺的这个图形是正六边形,则这张矩形纸片的宽和长之比为 . 
参考答案:
【答案】![]() :2
:2
【解析】解:作OB⊥AD,根据已知可以画出图形, 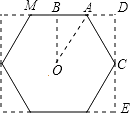
∵根据折叠方式可得:
AB=AD,CD=CE,∠OAB=60°,AO等于正六边形的边长,
∴∠BOA=30°,
∴2AB=AO,![]() =tan60°=
=tan60°= ![]() ,
,
∴BO:AM= ![]() :2.
:2.
所以答案是: ![]() :2.
:2.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
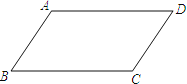
查看答案和解析>>【题目】如图,AB∥CD,AD∥BC,∠A﹦3∠B.求∠A、∠B、∠C、∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师从“淋浴龙头”受到启发.编了一个题目: 在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当m=
 时,求n的值.
时,求n的值.
你解答这个题目得到的n值为( )
A.4﹣2
B.2 ﹣4
﹣4
C.
D.
-
科目: 来源: 题型:
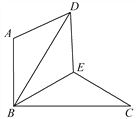
查看答案和解析>>【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,相距2cm的两个点A、B在直线l上.它们分别以2cm/s和1cm/s的速度在l上同时向右平移,当点A,B分别平移到点A1 , B1的位置时,半径为1cm的⊙A1 , 与半径为BB1的⊙B相切.则点A平移到点A1 , 所用的时间为s.
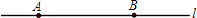
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A
 B
B C
C ;
;(2) 请画出△ABC关于原点对称的△A
 B
B C
C ;
;(3) 在
 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下面各题
(1)计算: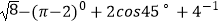
(2)先化简.再求值:a(a﹣2b)+2(a+b)(a﹣b)+(a+b)2 , 其中a=﹣ ,b=1.
,b=1.
相关试题

