【题目】先阅读下面的知识,后解答后面的问题:
探究:如图,在△ABC中,已知∠B=∠C,求证:AB=AC.

证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C, , , 所以△ABD≌△ACD( ),所以AB=AC.
(1)完成上述证明中的空白;
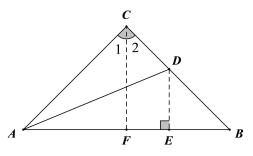
(2)已知如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB.试问:AC+CD与AB相等吗?说明理由.

参考答案:
【答案】(1)![]() ,AD=AD,AAS;(2)AC+CD=AB,理由见解析.
,AD=AD,AAS;(2)AC+CD=AB,理由见解析.
【解析】
(1)根据AAS可判定△ABD≌△ACD,进而完成填空;
(2)过点D作DE⊥AB,垂足为E,如图,先用AAS证明△ACD≌△AED,得到AC=AE,再作∠ACB的平分线CF交AB于点F,利用SAS证明△ACF≌△BCF,得到∠CAB=∠B,进一步通过三角形的内角和得出∠DEB=∠B,进而根据探究结论推出ED=EB,即可证得结论.
解:(1)证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C,![]() , AD=AD ,
, AD=AD ,
所以△ABD≌△ACD(AAS),
所以AB=AC.
故答案为:![]() ,AD=AD,AAS.
,AD=AD,AAS.
(2)AC+CD=AB,理由如下:
过点D作DE⊥AB,垂足为E,如图,则∠AED=90°,
∵∠ACB=90°,∴∠ACB=∠AED,
∵AD平分∠CAB,∴∠CAD=∠EAD,
在△ACD和△AED中,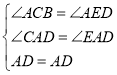
∴△ACD≌△AED(AAS).
∴AC=AE,CD=ED,
作∠ACB的平分线CF交AB于点F,则∠1=∠2,
在△ACF和△BCF中,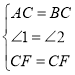
∴△ACF≌△BCF(SAS),∴∠CAB=∠B,
∵∠ACB=90°,∴∠CAB=∠B=45°,
∴∠DEB=90°-∠B=45°,
∴∠DEB=∠B,
由探究结论知:ED=EB.
∴BE=CD,
∴AB=AE+BE=AC+CD.
-
科目: 来源: 题型:
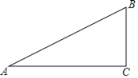
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,直接写出∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
-
科目: 来源: 题型:
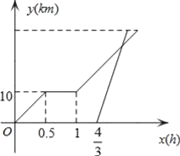
查看答案和解析>>【题目】周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.
下列说法正确的有( )个
①小明骑车的速度是20km/h,在甲地游玩1小时
②小明从家出发
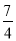 小时后被妈妈追上
小时后被妈妈追上③妈妈追上小明时离家25千米
④若妈妈比小明早10分钟到达乙地,则从家到乙地30km.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为矩形ABCD外一点,AE=DE,连接EB、EC分别与AD相交于点F、G.求证:
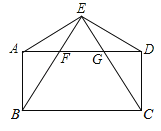
(1)△EAB≌△EDC;
(2)∠EFG=∠EGF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组6名同学参加一次知识竞赛,共答20道题,每题分值相同,答对得分,答错或不答扣分,下面是前5名同学的得分情况(如下表):

(1)表中的m = ,n = ;
(2)该小组第6名同学说:“这次知识竞赛我得了0分”,请问他的说法是否正确?如果正确,请求出这位同学答对了多少题;如果不正确,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列不等式(组),并把解集在数轴上表示出来
(1)3x﹣5<2(2+3x)
(2)

(3)

(4)

相关试题

