【题目】如图,点E为矩形ABCD外一点,AE=DE,连接EB、EC分别与AD相交于点F、G.求证: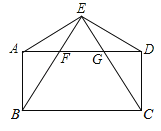
(1)△EAB≌△EDC;
(2)∠EFG=∠EGF.
参考答案:
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题分析:(1)先根据四边形ABCD是矩形,得到AB=DC,∠BAD=∠CDA=90°.再根据EA=ED,得到∠EAD=∠EDA,由等式的性质得到∠EAB=∠EDC.利用SAS即可证明△EAB≌△EDC;
(2)由△EAB≌△EDC,得到∠AEF=∠DEG,由三角形外角的性质得出∠EFG=∠EAF+∠AEF,∠EGF=∠EDG+∠DEG,即可证明∠EFG=∠EGF.
试题解析:(1)∵四边形ABCD是矩形,∴AB=DC,∠BAD=∠CDA=90°.∵EA=ED,∴∠EAD=∠EDA,∴∠EAB=∠EDC.在△EAB与△EDC中,∵EA=ED,∠EAB=∠EDC,AB=DC,∴△EAB≌△EDC(SAS);
(2)∵△EAB≌△EDC,∴∠AEF=∠DEG,∵∠EFG=∠EAF+∠AEF,∠EGF=∠EDG+∠DEG,∴∠EFG=∠EGF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星光服装厂接受生产一些某种型号的学生服的订单,已知每3m长的某种布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用750m长的这种布料生产学生服,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠A=30°.
(1)作线段AB的垂直平分线DE,垂足为点E,交AC于点D,要求用尺规作图,保留作图痕迹,标注有关字母,不要求写作法和证明;
(2)连接BD,直接写出∠CBD的度数;
(3)如果△BCD的面积为4,请求出△BAD的面积.
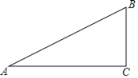
-
科目: 来源: 题型:
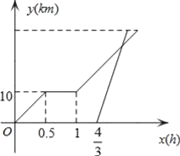
查看答案和解析>>【题目】周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.
下列说法正确的有( )个
①小明骑车的速度是20km/h,在甲地游玩1小时
②小明从家出发
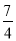 小时后被妈妈追上
小时后被妈妈追上③妈妈追上小明时离家25千米
④若妈妈比小明早10分钟到达乙地,则从家到乙地30km.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的知识,后解答后面的问题:
探究:如图,在△ABC中,已知∠B=∠C,求证:AB=AC.

证明:过点A作AD⊥BC,垂足为D, 在△ABD与△ACD中,
∠B=∠C, , , 所以△ABD≌△ACD( ),所以AB=AC.
(1)完成上述证明中的空白;
(2)已知如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠CAB.试问:AC+CD与AB相等吗?说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组6名同学参加一次知识竞赛,共答20道题,每题分值相同,答对得分,答错或不答扣分,下面是前5名同学的得分情况(如下表):

(1)表中的m = ,n = ;
(2)该小组第6名同学说:“这次知识竞赛我得了0分”,请问他的说法是否正确?如果正确,请求出这位同学答对了多少题;如果不正确,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
相关试题

