Question

【题目】解下列不等式（组），并把解集在数轴上表示出来

（1）3x﹣5＜2（2+3x）

（2）

（3）

（4）

Answer 1

【答案】(1)x＞﹣3，(2)x≤4，(3)x＞2，(4)﹣＜x＜1．数轴见解析

【解析】

（1）根据解一元一次不等式基本步骤：去括号、移项、合并同类项、系数化为1可得．

（2）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．

（3）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．

（4）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．

（1）3x﹣5＜4+6x，

3x﹣6x＜4+5，

﹣3x＜9，

x＞﹣3，

将解集表示在数轴上如下：

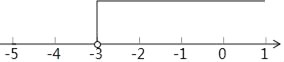
（2）3x﹣6≤2（7﹣x），

3x﹣6≤14﹣2x，

3x+2x≤14+6，

5x≤20，

x≤4，

将解集表示在数轴上如下：

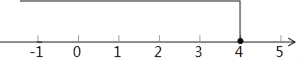
（3）解不等式5（x﹣2）﹣1≤8（x﹣1）得：x≥﹣1，

解不等式5（x﹣1）＞2x+1，得：x＞2，

则不等式组的解集为x＞2，

将解集表示在数轴上如下：

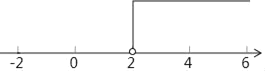
（4）解不等式6x﹣2＞3x﹣4，得：x＞﹣，

解不等式＜1，得：x＜1，

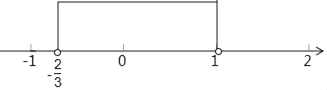
则不等式组的解集为﹣＜x＜1．

将解集表示在数轴上如下：