【题目】要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.

(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接指出甲,乙这10次射击成绩的方差s甲2,s乙2哪个大?
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选哪位参赛更合适?为什么?如果其他班级参赛选手的射击成绩都在9环左右,本班应该选哪位参赛更合适?为什么?
参考答案:
【答案】(1)8环;(2)s甲2>s乙2;(3)答案见解析.
【解析】分析:(1)根据平均数的计算公式和折线统计图给出的数据即可得出答案;
(2)根据图形波动的大小可直接得出答案;
(3)根据射击成绩都在7环左右的多少可得出乙参赛更合适;根据射击成绩都在9环左右的多少可得出甲参赛更合适.
本题解析:
解:(1)乙的平均成绩是:(8+9+8+8+7+8+9+8+8+7)÷10=8(环);
(2)根据图象可知:甲的波动小于乙的波动,则s甲2>s乙2;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选乙参赛更合适;因射击成绩在7环以上的次数乙比甲多,所以乙参赛获胜可能性更大;
如果其他班级参赛选手的射击成绩都在9环左右,本班应该选甲参赛更合适.因射击成绩在9环以上的次数甲比乙多,所以甲参赛获胜可能性更大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 ,
, ,
, 分别是边
分别是边 ,
, ,
, 上的点,且
上的点,且 ,
, ,
, 相交于点
相交于点 ,若点
,若点 是
是 的重心.则以下结论:①线段
的重心.则以下结论:①线段 ,
, ,
, 是
是 的三条角平分线;②
的三条角平分线;② 的面积是
的面积是 面积的一半;③图中与
面积的一半;③图中与 面积相等的三角形有5个;④
面积相等的三角形有5个;④ 的面积是
的面积是 面积的
面积的 .其中一定正确的结论有( )
.其中一定正确的结论有( )
A.①②③B.②④C.③④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB=4
 ,AC⊥AB,BD⊥AB,AC=BD=3
,AC⊥AB,BD⊥AB,AC=BD=3 .点 P 在线段 AB 上以 1
.点 P 在线段 AB 上以 1 的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为
的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为  (s).
(s).(1)若点 Q 的运动速度与点 P 的运动速度相等,当
 =1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;
=1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点 Q 的运动速度为

 ,是否存在实数
,是否存在实数 ,使得△ACP 与△BPQ 全等?若存在,求出相应的
,使得△ACP 与△BPQ 全等?若存在,求出相应的 、
、 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
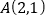 ,
,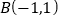 ,
,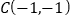 ,
,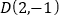 ,把一根长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在
,把一根长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在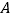 处,并按
处,并按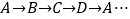 的规律紧绕在四边形
的规律紧绕在四边形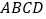 的边上,则细线的另一端点所在位置的坐标是__________.
的边上,则细线的另一端点所在位置的坐标是__________.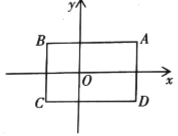
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校美术组要购买铅笔和橡皮,按照商店规定,若同时购买60支铅笔和30块橡皮,则需按零售价购买,共需支付30元;若同时购买90支铅笔和60块橡皮,则可按批发价购买,共需支付40.5元.已知每支铅笔的批发价比零售价低0.05元,每块橡皮的批发价比零售价低0.10元.求每支铅笔和每块橡皮的批发价各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E、F、G. H分别AB、BC、 CD、 DA边上的动点,且AE=BF=CG=DH

(1)求证:四边形EFGH是平行四边形:
(2)在点E、F、G、H运动过程中,判断直线GE是否经过某一定点,如果是,请你在图中画出这个点:如果不是,请说明理由.
相关试题

